RESUMO

Analisam-se particularidades inerentes ao estudo dos estrabismos, tais como as dificuldades para suas definições e os diferentes modos com os quais eles podem ser concebidos, a relatividade com que as posições binoculares possam ser interpretadas e os elementos referenciais necessários para a circunscrição dessas questões. A partir daí, discute-se o conceito de posição primária do olhar e as condições de sua operacionalização, concluindo-se pela impossibilidade de concretização desse ponto "zero", a partir do qual seriam feitas as medidas dos estrabismos e as quantificações de movimentos oculares. A seguir, passa-se ao exame da construção dos múltiplos sistemas referenciais aplicáveis à quantificação dos estrabismos, de cuja falta de consenso sobre qual deles usar decorrem implicações práticas elementares, como a falta de padronização do modo de superposição ortogonal de prismas, para a medida de desvios combinados, horizontal e vertical. Comenta-se a assimetria funcional das rotações oculares e suas exceções. Também se analisa a precisão com que se pode fazer a medida de um estrabismo, levando à conclusão sobre a impropriedade de uso de medidas fracionárias com as unidades angulares mais comumente usadas. Finalmente, são comentados alguns problemas técnicos dessas avaliações, tais como o das dificuldades operacionais relacionadas à dioptria-prismática, os subordinados ao uso de prismas e os da ocorrência de efeitos prismáticos pelo uso de lentes convencionais.

Descritores: Estrabismo; Eletrofisiologia; Córtex visual; Convergência ocular; Acomodação ocular; Medições dos movimentos oculares

ABSTRACT

Some particular points concerning the study of strabismus are analyzed, specially, the difficulties for definitions and the different ways it can be conceived, besides the relativity of binocular positions interpretation, and the necessary referential elements for circumscribing such questions. Then, the concept of primary position of gaze is discussed as well as the conditions for its operational attainment, leading to the conclusion that it is materially impossible to achieve this "zero" point, from which all other measurements of strabismus or ocular movements should be done. In sequence, the construction of multiple referential systems applying the quantification of strabismus are examined. The lack of consensual agreement about which should be used as the standard system causes elementary practical implications, as the lack of agreement about how to superimpose orthogonal prisms for the measurement of associated horizontal and vertical deviations. The functional asymmetry of ocular rotations and its exceptions are commented. The accuracy that the measurements of strabismus can be performed is analyzed, leading to the conclusion that fractional figures using the commonest angular unities are improper. At last, some technical problems related to such evaluations are also commented, as operational difficulties related to prism-diopter unity, concerning the use of prisms, and prismatic effects due to the use of conventional optical glasses.

Keywords: Strabismus; Electrophysiology; Visual cortex; Convergence, ocular; Accommodation, ocular; Eye movement measurements

---

 

 

INTRODUÇÃO

Seria lógico esperar que o homenageado com a distinção de proferir conferência magna apresentasse nessa exposição a sinopse dos tópicos mais relevantes de sua trajetória acadêmica, com os quais julgasse haver mais contribuído para o avanço e a consolidação de conhecimentos em sua área de atuação. Mas, ao contrário, não me referirei a eles, conquanto, obviamente, não possa deixar de discorrer sobre temas relacionados aos estrabismos, os ocupantes de parte substancial de minha mente. Escolho conjeturar sobre a estrutura de conceitos pelos quais se fundamentam as aplicações diagnósticas e terapêuticas no atendimento dessas afecções, sobre procedimentos com que tais concepções são operadas e sobre suas respectivas limitações.

De fato, até sobre a própria definição de estrabismo, cujo rigor formal deveria claramente delimitar a extensão e o significado do termo, não há consenso. E, mais, nem sequer se delineia um entendimento comum sobre quais fatores devam prevalecer na construção dessa exigência elementar. Em obra recente⁽¹⁾, por exemplo, o desafio de como definir estrabismos foi examinado ao longo da história e entre oftalmologistas considerados como experientes na prática de entendê-los, resultando múltiplas respostas, nenhuma delas idêntica a outra; e que, embora com pontos de aproximação, mostravam importantes variações sobre critérios de abordagem do problema. A raiz disso é que a teoria e a prática sobre os estrabismos revelam uma relação recíproca de causas e efeitos, cujos elementos são tão íntima e completamente interdependentes - os do sistema oculomotor e os do sistema sensorial visual - que raramente se pode dissociá-los. De qualquer modo, consequências sensoriais dos estrabismos (como a diplopia ou a ambliopia) ou as motoras (acarretando distúrbios fisionômicos) não são necessárias, nem suficientes, como atributos de sua definição. Por outro lado, as delicadezas de interação dessas condições com as da normalidade, acarretam diferenciações pouco nítidas entre o que seja um ou outro estado. E, mais ainda, depende-se de admitidas duplicidades de critérios na caracterização dos estrabismos, de medidas "objetivas" e "subjetivas", de correções dirigidas à "funcionalidade" ou à "estética", chega-se a aparentes paradoxos, como o de que possa haver estrabismo sem parecer (ou sem se mostrar como) estrabismo e, ao contrário, de normalidade com a aparência de estrabismo (pseudoestrabismo). Contudo, dificuldades desse porte não devem dissuadir quem se debruce sobre esse tema de estudo mas, opostamente, suscitar o interesse para superá-las.

Além disso, limites absolutos entre estrabismo e normalidade, conquanto possam ser postulados, não chegam a ser determináveis. Tal zona de incerteza do conhecimento (ou, pelo menos, de delimitação de critério de estado) é de extensão variável, principalmente em conformidade ao rigor ou à tolerância de quem a observa. Com efeito, entre a concepção teórica do que deva ser caracterizado como estrabismo e o resultado do procedimento usado para formalizá-la, cabe um distanciamento, tanto maior quanto mais estrito for o rigor dos princípios e fundamentos aplicados e a precisão dos métodos para objetivá-los.

Para a discussão dessas questões iniciais serão pois abordados os critérios de definição dos estrabismos e a distinção de suas propriedades (como anormalidades), relativamente ao que se considera normal, além das dificuldades operacionais de caracterização dessas condições limítrofes.

 

CARACTERIZAÇÃO DOS ESTRABISMOS: ASPECTOS CONCEITUAIS

A) Definição

Entre as diversas manifestações possivelmente encontradas nos estrabismos, a de ocorrência comum a todos - e que, por isso, deve constar em suas definições - é o defeito de posicionamento binocular, ou seja, o defeito de posicionamento de um olho, relativamente ao outro. De qualquer modo, por sua concepção semiótica, ainda sem o poder de se alçar à condição de definição, o significado de estrabismo, essencialmente empírico - ao ensejar as proposições de olho(s) e posição - torna-se redutível a uma conjetura relativística, pressupondo a necessidade de assunção de um referencial (em função do qual o posicionamento binocular possa ser atribuído). Assim, o que se entende por olho (e, por consequência, sua posição relativamente ao referencial) deve ser convenientemente estabelecido.

1) O conceito de posição ocular e sua dualidade essencial

A primeira dicotomia analítica sobre o conceito de estrabismo resulta do que se subordina à abstração de "olho". Heuristicamente, e partindo-se do princípio de que olho existe para olhar (e, daí, ver)(¹), chega-se à primeira vertente da concepção dos estrabismos, a que se refere a condições psicofísicas e perceptuais que lhe são inerentes. Nesse caso, sabe-se que a imagem de um objeto a ser visualmente discriminado (e que será assumido como o primeiro "referencial"), com o máximo detalhamento, deve se formar sobre a região de maior densidade de fotorreceptores, a fovéola, no centro da fóvea, por isso considerada como o centro (funcional) da retina, isto é, "o olho". Na verdade, a imagem óptica do objeto pode não estar sobre a fovéola (a condição buscada, ponto F, Figura 1), mas adiante dela (miopia, ponto M, Figura 1), ou "atrás" (²) da retina (hipermetropia, ponto H, Figura 1).

 

 

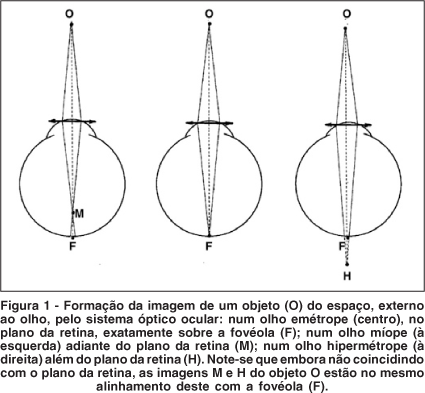
Assim, o olho pode ser reduzido a um ponto (no centro da fovéola), estabelecendo-se entre ele e um outro ponto do objeto de atenção visual no espaço (o referencial) uma linha reta imaginária, o eixo visual. Ao invés da "posição do olho relativamente ao ponto referencial do espaço", pode-se falar, alternativamente, de direcionamento do olho (ou melhor, do eixo visual) entre o centro da fovéola e esse ponto referencial (objeto de atenção visual). Embora merecendo aprofundamentos adicionais, aos quais se retornará mais adiante, essa proposição deve ser preliminarmente acolhida para permitir a continuidade da discussão conceitual dos estrabismos, em termos mais abrangentes.

Mas há circunstâncias, pelas mais variadas razões, em que o olho, embora exista, não cumpre as funções que dele se espera: nem sempre ele olha (e, daí, "vê"). Assim, ainda que ocasionalmente, o centro da fovéola não pode ser (sempre) tomado como atributo de representação do "olho": ou por, simplesmente, inexistir (por exemplo, em cicatrizes centrais de coriorretinites); ou por, mesmo presente, não funcionar (por exemplo, em cegueiras corticais). Nesses casos, não mais se aplica o princípio de que "o olho existe para olhar", cabendo agora o de que "o olho existe para ser olhado" (ou "visto"). Ou seja, inverte-se o critério: de observador (ao referencial) o "olho" examinado passa a observado (a partir de um ponto referencial). Muda-se, também, a representação do direcionamento ocular (estimado a partir desse ponto de observação), elegendo-se, para tal, uma linha que passe, perpendicularmente, do centro da pupila e pelo centro da córnea (obviamente, quando pupila e córnea puderem ser estimadas como "centradas"), o chamado eixo pupilar.

Ora, o eixo visual e o pupilar não são, necessariamente, coincidentes e, aliás, quase sempre discrepantes, diferindo por um ângulo (chamado kappa, K), costumeiramente descrito como com valores entre 3 e 7º mas chegando, em alguns casos, a alcançar magnitudes maiores. Qual desses valores deva prevalecer, se o sensorial, ou "funcional" (o olho com órgão da visão), se o "estético" (o olho como componente fisionômico), ou seja, qual direcionamento axial (o visual ou o pupilar) se deva tomar como princípio para o relacionamento binocular, constitui a primeira questão a se estabelecer, para a definição de estrabismo.

É claro que a escolha de qual dos eixos oculares deva prevalecer para a caracterização do estrabismo não é arbitrária, mas condicionada ao estado funcional de cada um dos olhos, separadamente. Por exemplo, a diferença entre os posicionamentos dos eixos visuais (ao ponto referencial) justifica o que se conhece como ângulo objetivo (da medida) do estrabismo (E), enquanto a diferença entre os direcionamentos dos eixos pupilares (ao ponto referencial) representa o ângulo de aparência do estrabismo (A). Como entre eles há um ângulo (kappa, K), o resultado binocular é:

E_D = A_D + K_D
E_E = A_E + K_E
E = A + K

Ou seja, pode haver um estrabismo, mascarado por um ângulo kappa de sinal contrário, anulando a aparência de desvio e dando a noção de uma posição binocular adequada (embora haja o desvio); ou, ao contrário, detectar-se um desvio aparente (pseudoestrabismo), causado por eixos pupilares angulados entre eles quando, na verdade, os eixos visuais acham-se corretamente posicionados relativamente ao objeto visado (E=0).

2) O conceito de estrabismo: relativização ao referencial

Uma vez determinada a posição de cada olho (centro da fovéola, ou o centro da pupila), relativamente ao referencial (respectivamente, o ponto observado, ou o ponto de observação), isto é, as direções de cada um dos eixos (respectivamente, os visuais, ou os pupilares), conceitua-se o estrabismo como a diferença entre os alinhamentos esperados. Ou seja, o ângulo entre os direcionamentos oculares. Em outros termos, como um distúrbio da relação posicional binocular, com referência a um ponto (normalmente, o objeto para o qual os olhares são dirigidos).

Um simples esquema ilustra a relatividade do conceito de estrabismo (e de seu sentido), ou de normalidade, dependendo de como as três referências (os dois olhos e o objeto de atenção visual, ou o ponto de observação) se combinam (Figura 2).

 

 

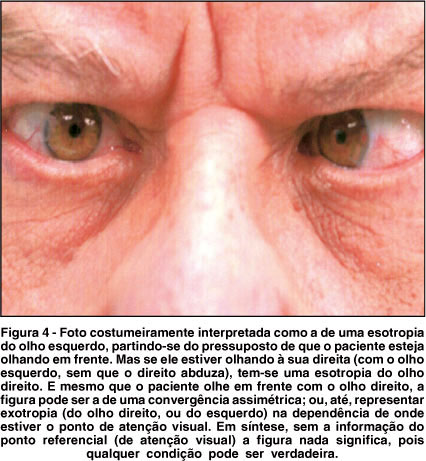
Por essa figura, nota-se que para a mesma relação de direcionamentos (ou "posicionamentos") oculares, várias condições podem ser supostamente verdadeiras, desde esotropias (do olho direito, ou do esquerdo), a exotropias (idem), ou ortotropia. O fator determinante da alternativa correta é, pois, a posição do referencial (o ponto de atenção visual, no caso de consideração dos eixos visuais, ou o ponto de observação, no caso de consideração dos eixos pupilares). Em síntese, o critério preliminar para conhecimento da posição de cada olho é essa referência no espaço. Para a qual se pressupõe que pelo menos um dos olhos esteja alinhado, isto é, com o eixo visual (ou o pupilar) dirigido ao objeto referencial (Figura 3). Em princípio, portanto, sem esses conhecimentos, não é tecnicamente possível dizer que a figura 4 represente uma esotropia do olho esquerdo (a menos que fique implícito que o paciente esteja olhando para o centro da lente da câmara fotográfica), ou do direito (hipótese verdadeira, se se souber que o paciente olha para a direita), nem se pode excluir que se trate de uma posição normal de convergência assimétrica ou, enfim, até mesmo uma de exotropia.

 

 

3) O fator sensorial

Mas outro fator deve ser ainda considerado, o do estado da funcionalidade sensorial binocular, isto é, de como se faz a percepção subjetiva do espaço, iniciada pelos dois olhos, "simultaneamente". Cria-se, então, um terceiro conceito de avaliação, o do desvio subjetivo (S), além do de desvio "real" ou objetivo (E) e do de aparência (A). Com isso, define-se a chamada correspondência visual, ou retínica, normal (quando E=S) ou anômala (quando E ≠ S), independentemente de A.

O desvio subjetivo (S) é determinado não mais pelos eixos visuais, mas por suas correspondentes direções visuais no fenômeno binocular de percepção do espaço. Ou seja, em que direções egocêntricas (assim chamadas por se referirem à pessoa examinada como fonte de informação) tornam-se subjetivamente percebidas as direções dos eixos visuais (objetivamente determináveis). Desse modo, e diferindo do estado da aparência fisionômica conferida pela posição dos eixos pupilares (A), estrabismos podem ser expressamente qualificados e quantificados por critérios objetivos (E) e subjetivos (S), nem sempre coincidentes e cujas eventuais discrepâncias são elementos substantivos em suas caracterizações e estratégias de abordagem.

Em resumo, estrabismos podem ser caracterizados por diferentes "ângulos de desvio" da normalidade, de acordo com a "realidade" que se queira exprimir: entre as direções do olhar (eixos visuais, ângulo objetivo), entre as direções em que são projetadas no espaço as imagens do objeto de atenção visual, formadas em cada olho (percepção sensorial, ângulo subjetivo) e entre as direções às quais os olhares aparentemente estão dirigidos (eixos pupilares, ângulo aparente). Dessa multiplicidade de critérios, dos fatores que lhes são concernentes, e das complexidades das respectivas interações, derivam as possíveis dificuldades de se uniformizar a definição dos estrabismos.

B) Elementos da definição

1) O eixo visual

Assim, para a definição do que seja o ângulo "objetivo" de um estrabismo de consideração "funcional", preceitua-se o alinhamento dos olhos (fovéolas) ao objeto referencial de atenção visual (o objeto de fixação), alinhamento esse subordinado ao conceito de eixo visual.

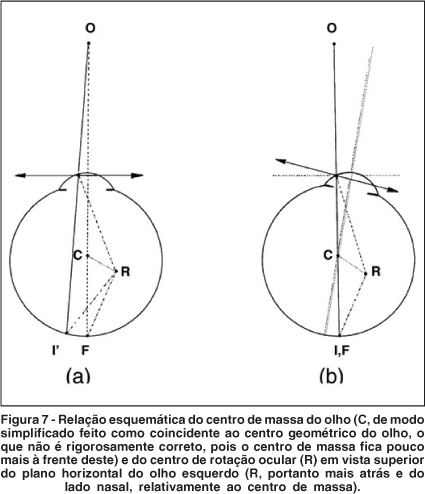
Como abstração geométrica, essa linha reta unindo cada fovéola ao objeto de fixação não possui correspondentes físicos. Ela não se confunde com o conceito de eixo óptico, frequentemente utilizado para as relações ópticas do modelo idealizado de um sistema ocular centrado (o do olho esquemático), mas fictício, devido a assimetria (ainda que pequena) de alinhamento dos dioptros que o constituem. Nem, tampouco se equipara à chamada linha de visada (ou de visão), que une o ponto de fixação ao centro da pupila de entrada do sistema óptico ocular. Nem, ainda, ao eixo geométrico do olho (indeterminável na prática) (Figura 6). E embora, finalmente, represente a linha imaginária de direcionamento ocular, não se condiciona como equivalente à linha referencial de medidas das rotações oculares. Com efeito, por não passar necessariamente pelo centro de rotação ocular (aliás, geralmente tido como excêntrico ao próprio olho), mudanças de direcionamento dos eixos visuais e as respectivas rotações oculares que as produzem, não são idênticas (Figura 7).

 

 

 

 

 

 

2) Objetivação do eixo visual

Entretanto, a posição espacial do eixo visual, ou pelo menos a de construção de seus componentes, depende do sistema óptico ocular (que gera a imagem foveal do objeto fixado) e de suas relações com o centro de rotação ocular respectivo. Com efeito, um sistema óptico ao ser descentrado altera o posicionamento da imagem de um objeto (Figura 5) e se a descentração ocorrer no olho alterar-se-ão as relações originais dos eixos oculares (geométrico, óptico, pupilar) com o eixo visual, modificando (gerando, ou aumentando, ou diminuindo), por exemplo, um ângulo kappa (Figura 6).

De fato, pela figura 5, se componentes do sistema óptico ocular forem transladados no plano frontal ("descentrados"), a imagem do objeto O não mais se forma sobre a fovéola (I, Figura 5a), mas em outro ponto da retina (I', Figura 5b); ou, alternativamente, a imagem que se forma sobre a fovéola (I) é a de um outro ponto do espaço (O', Figura 5c). Por consequência, então, o eixo visual não dependeria essencialmente da posição de O, mas da apropriada centração do sistema óptico ocular. Caso contrário (descentração), o referencial (o objeto cuja imagem se forma sobre a fovéola) passaria a ser outro (O'). Ora, essas conjeturas seriam adequadas se o olho (a fovéola) fosse imóvel. Mas esse não é o caso: a fovéola pode voltar a receber a imagem de O (que, portanto, pode continuar a ser tratado como referencial) por um ajustamento direcional do olhar (Figuras 6, 7 e 8).

 

 

A "descentração" do sistema óptico determinada pela não coincidência dos eixos ópticos principais dos diferentes dioptros, acarreta duas consequências principais. Uma é a da perda da coaxialidade das linhas de direção correspondentes do "eixo" visual, isto é, a do espaço objeto (do objeto referencial do "olhar" ao primeiro ponto nodal, ou ponto nodal objeto - ou anterior - do sistema óptico ocular) e a do espaço imagem (do centro da fóvea ao segundo ponto nodal, ou ponto nodal imagem - ou posterior). Essa perda de coaxialidade entre os eixos visuais objeto e imagem, então feitos paralelos, tem sido negligenciável para um interstício (distância entre os pontos nodais objeto e imagem) da ordem de 0,25 mm. Com uma translação de 0,3 mm da linha imaginária, única, entre a fóvea e um ponto situado a 5 metros à frente do plano principal anterior do olho, a correção angular necessária seria de apenas 12,3". Mas se o objeto estiver 30 cm à frente do plano principal anterior do olho, a diferença alcança 3' 12" (³).

A outra consequência é a do efeito prismático produzido pelo sistema óptico "descentrado". Nesse caso (Figura 6) os efeitos são muito mais pronunciados.

Também importante nessa construção do eixo visual é a posição da pupila, a abertura que limita a entrada de luz no olho. Como abertura do sistema óptico, a pupila determina a posição da imagem de um objeto por ele formada e, pois, influencia em como o eixo visual deva estar direcionado. Daí a concepção de "linha de visão", a que se estende do centro da pupila de entrada (⁴) ao objeto do olhar⁽³⁾. Em condições de visão normal, com um sistema óptico perfeitamente centrado, essa linha representa a direção do eixo visual. Mas uma pupila muito descentrada (corectopia) pode inviabilizar a formação da imagem foveal de um objeto "em frente" do olho, isto é, impedir que o eixo visual passe por ela. De qualquer modo, a linha reta, imaginária, do objeto à fóvea, não passa necessariamente pelo centro das pupilas de entrada e de saída (Figura 9).

Finalmente, ainda que seja costumeiro considerar que se possa "objetivar" a posição do eixo visual (e, assim, "objetivar" as medidas do estrabismo e das rotações oculares) ao se pedir que a pessoa examinada "fixe" (visualmente) um ponto do espaço, essa condição é, em sua essência, absolutamente dependente do sujeito observado, não do observador. Tais avaliações não são, portanto, rigorosamente objetivas, pois a pessoa examinada, eventualmente:

a) não fixa especificamente o referencial solicitado. É óbvio que se pode solicitar que ela discrimine minúcias de uma figura, ou texto, para comprovar que a respectiva imagem retínica esteja se formando sobre a fóvea; mas essas imagens não são puntiformes (o que gera imprecisão), nem há garantias de que a fixação, uma vez "confirmada", permaneça; ou, ainda, que o olho retorne à situação original, se houver mudança de fixação (aliás, uma técnica de exame rotineira). Essa falta de resposta adequada pode ser voluntária, ou involuntária (apraxias, ideativas ou ideomotoras). O próprio reflexo automático de fixação, ou de refixação, pode estar comprometido.

b) Não colabora adequadamente nessa fixação requerida, por defeito óptico (ametropias, perdas de transparência), ou sensorial visual; ou, ainda, por falta de estabilidade motora (nistagmos).

C) Precisão das medidas e seus limites

1) Considerações anatômicas

Elementos funcionais da retina, os chamados campos receptivos, limitam a capacidade de resolução visual do espaço na dependência de seus tamanhos. Os centrais, foveolares, como as menores estruturas sensoriais da retina, correspondem à superfície de um único cone fotorreceptor. Essa estrutura, com diâmetro de aproximadamente 2 μm equivale, relativamente ao ponto nodal imagem do sistema óptico de um olho padrão (situado a 17,055 mm à sua frente, pelo olho esquemático de Gullstrand)⁽²⁾ a um ângulo de 24". Tal seria o limite teórico da resolução discriminativa visual, apenas por considerações anatômicas. Sendo essa, portanto, a menor separação angular que se pode perceber entre dois pontos no espaço, não é concebível que um movimento ocular voluntário alcance extensões menores.

2) Considerações ópticas

Outra objeção sobre o eixo visual diz respeito à proposição axiomática de sua construção como "linha". Independentemente de quaisquer outros possíveis defeitos do sistema óptico ocular, a própria natureza ondulatória da luz determina, sobre a retina, não uma imagem também puntiforme, mas círculos de difusão da luz, pelo fenômeno da difração. Assim, por exemplo, o tamanho diametral (D=2 r) de diferentes círculos de difração (m=1... 2... etc.) em função do diâmetro da abertura (d), do comprimento de onda da luz incidente (λ) e da distância entre a abertura considerada e a captação da imagem (q) é dado pela equação:

r=2 m. λ. q / π. d

Para o raio (r) do primeiro círculo de difração (m=1) na retina, isto é, para a distância entre o centro (iluminado) da imagem difratada de um ponto de luz e a margem do primeiro círculo de interferência negativa (escuro), o que representa o poder de resolução do sistema óptico ocular, aplica-se a equação de Rayleigh (em que f é a distância focal do sistema óptico ocular)^(4-5):

r=1,22 f. λ / d

Para uma pupila de 6 mm de diâmetro (d=6), num olho "normal" (f=17,055 mm, conforme valores de Gullstrand)⁽²⁾ e para a luz amarela (λ=5893.10^-7 mm), vem r=2,044 μm o que, praticamente, coincide com o diâmetro de um cone fotorreceptor. (Para outros círculos de espalhamento da luz, os diâmetros são, obviamente, maiores). Ou seja, a um ponto objeto do espaço, não corresponde um ponto imagem na retina. E embora se possa manter o postulado de um eixo visual unindo o ponto objeto no espaço ao centro de sua imagem difratada, na retina, a fisiologia da retina conduz a implicações práticas, limitando ainda mais a capacidade de resolução visual do olho e, consequentemente, a precisão com que uma relação puramente retilínea seja estabelecida entre esses dois pontos. De fato, para que dois pontos do espaço formem imagens cujos círculos de difração respeitem o tamanho de um cone (2 μm), a distância de seus centros (para as condições acima calculadas) deve ser de, no mínimo, (2,044/2) + 2 + (2,044/2) micrômetros, ou seja 4,044 μm. Isso corresponde a uma distância angular de 49".

3) Considerações mecânicas

Na verdade, as considerações anteriormente feitas estabelecem o limite de percepção da separação entre dois pontos do espaço e, pois, o limite do estímulo para que um movimento de mudança da fixação de um deles ao outro seja possível. Como visto, a magnitude dos círculos de difração depende do comprimento de onda da luz refratada (que, geralmente, não é monocromática), do tamanho da pupila e da distância focal do sistema óptico ocular, enquanto a anatomia da retina determina a capacidade discriminativa. Tudo pode ser resumido pela medida da acuidade visual (AV) que se define, exatamente, pela recíproca desse ângulo visual limite em minutos de arco (a), isto é, AV=1/a. Lembre-se, contudo, que esse ângulo é referido ao ponto nodal imagem do sistema óptico ocular (cerca de 17 mm à frente da fóvea), enquanto rotações são medidas relativamente ao centro de rotação ocular, mais próximo dela (cerca de 12,2 mm à sua frente). Assim, para o ângulo anteriormente calculado como de 49", o de rotação, em segundos de arco (w) entre os pontos correspondentes vale 68". De modo simplificado, pela exígua grandeza desses ângulos a relação entre eles pode ser tratada como linear:

17,055 a = 12,200 w .^.. 1,4 a ≈ w .^.. 84 / AV ≈ w (") .^.. 1,4 / AV ≈ w (')

Em suma, pode-se estimar que em função do valor da acuidade visual de uma pessoa, que corresponde ao mínimo ângulo com que dois pontos podem ser vistos separados, o estímulo visual para uma rotação voluntária entre eles não pode ser menor. Para uma acuidade visual padrão (AV=1,0) esse ângulo é de 84" ou 1,4'. Para uma acuidade visual 0,7, o valor de w é 120" ou 2'.

4) Instabilidade ocular fisiológica

Sabe-se, entretanto, que o olho não se mantém estavelmente dirigido a um ponto do espaço, durante sua fixação visual. "Micro"-oscilações, involuntárias, representadas por movimentos de diversas naturezas, com direções aleatórias, amplitudes e frequências irregulares, compõem um quadro de variabilidade posicional do eixo visual em torno do aludido ponto de "fixação" visual. Esses movimentos podem chegar a cobrir uma área de cerca de 100 μm de diâmetro, em torno do centro da retina⁽⁶⁾, o que corresponde a um ângulo (medido relativamente ao centro de rotação ocular) de, aproximadamente, 0,47º (≈ 28').

Experimentos mostraram que a distância angular mínima entre dois pontos do espaço cuja fixação possa ser voluntariamente mudada (por uma rotação sacádica)⁽⁷⁾ fica em torno de 18', ou seja, 0,3º. Assim, como não se pode garantir a mudança posicional do eixo visual entre esses pontos, a separação angular entre eles deve ser, portanto, considerada como a do menor movimento ocular voluntário que possa ser requerido.

D) Considerações sobre os sistemas referenciais de coordenadas

Uma vez estabelecidas as premissas pelas quais o posicionamento, ou o direcionamento, ocular no espaço possa ser conhecido, a consideração seguinte é sobre as possíveis mudanças dessas condições, a dos movimentos oculares.

Embora já se tenha convencionado um referencial para a definição do direcionamento do olhar, mas como ele pode ser, alternativamente, qualquer ponto do espaço, convém que se estabeleça um novo, um referencial fixo, a partir do qual aquele também passe a ser considerado e que sirva para qualificar e quantificar os movimentos oculares. Postula-se, para tal fim, o centro das rotações oculares.

Entretanto, essa é, igualmente, uma simplificação teórica da realidade, pois não há um ponto de todo o olho que fique absolutamente fixo relativamente a outro referencial do espaço (por exemplo, o das paredes ósseas orbitárias) durante qualquer um de seus movimentos. Para fins práticos, postula-se para representar esse conceito o centro de massa do olho, geralmente confundido com o centro geométrico do olho, mas não coincidente a ele, ficando-lhe a cerca de 1,3 mm atrás e 1,6 mm medialmente⁽³⁾ (Figura 7). Para expressar o que realmente ocorre, criou-se a concepção de um centrodo, a dos pontos ocupados por esse centro de rotação ocular, durante as rotações oculares, figurados relativamente a um referencial fixo do espaço, imaginário.

De qualquer modo, não faria sentido deixar de referir os movimentos do olho em relação a esse referencial, efetivamente fixo, como o dos eixos orbitários. De fato, com este sistema referencial externo ao olho é possível arbitrar-se uma origem sobre a qual se cruzem, ortogonalmente, os três eixos fundamentais do espaço físico, um vertical e dois horizontais, definidos pela anatomia corporal como, respectivamente, o súpero-inferior, SI (ou vertical), o látero-medial, LM (ou transversal) e o ântero-posterior, AP (ou longitudinal). Reciprocamente, esses eixos relacionam-se aos três planos fundamentais do espaço: o horizontal, perpendicularmente atravessado pelo SI e contendo os eixos LM e AP; o sagital, perpendicularmente atravessado pelo LM e contendo os eixos AP e SI; o frontal, perpendicularmente atravessado pelo AP e contendo os eixos SI e LM.

Igual sistema de eixos e de planos pode ser erigido para o olho, com sua origem passando pelo já comentado centro de massa, ou centro de rotação. Isso dá origem ao chamado sistema referencial dos eixos oculares.

Convém lembrar que o previamente escolhido referencial para conhecimento do alinhamento ocular ao objeto de atenção visual, o eixo visual, não necessariamente passa pelo "centro de rotação" ocular, tomado como a origem do sistema de eixos oculares; ou por um seu sucedâneo, efetivamente fixo, tomado como a origem do sistema de eixos orbitários. Mas isso não acarreta complicações conceituais adicionais, conforme ilustração pela figura 8, apenas o requerimento de correção do valor da rotação suscitada (entre O e P) para o da efetivamente realizada (ângulo r). Nessa figura, apesar do exagero desproporcional (proposital) no distanciamento do centro de rotação ocular (R) ao eixo visual (linha OF), isto é, o ângulo RFO=u, mas mantido na rotação r (para fixação do objeto P) pode-se deduzir que a respectiva rotação efetiva do eixo visual é idêntica a r, embora diferente da aparente (ângulo OFP=o). De fato, os triângulos RF'Y e HFY são congruentes: se o ângulo RFO e RF'P são iguais (u), assim como F'YR=FYH, então F'RF=r=FHY. Isto é, o ângulo de rotação da fóvea (FRF') é igual ao da rotação do eixo visual (OHP=FHY).

E) Posição primária do olhar

O marco zero do sistema oculomotor a partir do qual são consideradas as posições do olho para as eventuais medidas da magnitude angular de um estrabismo, ou as coordenadas (cartesianas, angulares, ou polares) de movimentos oculares é concebido como posição primária do olhar. É curioso que também sobre esse assunto não haja precisão na literatura pertinente. Na verdade, a definição dessa condição varia de autor para autor e, frequentemente, as referências achadas são, apenas, sobre modos de sua operacionalização. Mencionar, por exemplo, que posição primária do olhar corresponda ao "olhar em frente com a cabeça ereta" é surpreendentemente simplório. "Olhar em frente" indica tão somente uma direção (longitudinal, a do eixo visual) sem se importar se o eixo vertical (e, ou o horizontal) do olho está em posição "correta", isto é, sem torção. Obviamente, esta poderia ocorrer no "olhar em frente", tirando todo o significado de posição primária, mesmo que a cabeça permaneça "ereta". Aliás, essa afirmação também apenas significa que o plano horizontal da cabeça (órbita) coincide com um plano horizontal do espaço (o da Terra, no ponto em que a medida é realizada), mas não exclui a possibilidade de que ela (cabeça, órbita) esteja rodada para a direita ou para a esquerda (o olhar seria referido como "em frente" do corpo...). Outras tentativas de definição esbarram em incompletudes desse jaez.

Por outro lado, parece lógico que se condicione a posição primária do olhar como a de coincidência dos eixos oculares e orbitários. Porém, conquanto necessária, essa conjunção de fatores é ainda insuficiente para uma completa caracterização de posição primária. Ainda restaria circunscrever referenciais do corpo (eixos da cabeça e corpo alinhados ou, pelo menos, paralelos) e da gravidade. Agregar, por exemplo, "com a cabeça ereta" para se evitar a possibilidade de que a coincidência dos eixos oculares e orbitários se faça com a cabeça inclinada em relação ao corpo (como na manobra de Bielschowsky que, aliás, suscita estímulos labirínticos, por suas vezes indutores de torções oculares) não impede que o corpo fique inclinado relativamente à cabeça, com possíveis mensagens proprioceptivas de músculos do pescoço (e tronco) para a desestabilização inervacional a músculos oculares externos (Figura 10).

 

 

Contudo, se a influência gravitacional sobre o equilíbrio oculomotor for considerada pela referência de coincidência dos eixos orbitários e oculares com a linha de ação vertical, não se poderia falar em posição primária do olhar em um paciente deitado de costas (posição supina), ou de lado. É óbvio que os retos medial e lateral de um olho manterão condições de estase e de trabalho absolutamente diferentes das de se a pessoa examinada estiver deitada sobre seu lado direito, ou esquerdo, não apenas quanto à distribuição de forças em tal situação de repouso, como após o início de eventuais rotações oculares "horizontais". Certamente, todas essas posições não deixam de ser "primárias", mas requerendo que a condição corporal seja definida para diferenciá-las de outras (por exemplo, "posição primária do olhar em situação supina", ou "...em decúbito lateral esquerdo", etc.), cabendo à "normal" a definição de "coincidência dos eixos oculares e orbitários com a cabeça e corpo eretos" (isto é, com seus eixos verticais coincidentes às respectivas linhas de ação gravitacional).

Ora, se a "simples" posição primária do olhar já apresenta tais dificuldades conceituais, embora contornáveis, fica por outro lado praticamente inviável concretizar as condições operacionais de sua obtenção, a ponto de se chegar a renunciá-la como realidade tangível. De fato, num sistema de três eixos (ou planos) mutuamente ortogonais, basta a caracterização de dois deles para que o terceiro fique também conhecido. Todavia, a aparente ortogonalidade de linhas num dado plano não é suficiente para que se diga que elas sejam efetivamente ortogonais. Em outras palavras, a posição tridimensional de uma linha não pode ser conhecida, apenas, pelo exame de duas de suas três coordenadas espaciais (isto é, pelo conhecimento da projeção dessa linha num dado plano), requerendo-se que ela seja determinada num outro plano, perpendicular ao primeiro. Isso significa que não se pode afirmar a ortogonalidade de uma linha horizontal e outra vertical pela observação do plano frontal da cabeça (isto é, pelo exame da face).

As operações de materialização do conceito de posição primária do olhar apresentam outras ordens de dificuldades, que serão depois examinadas.

F) Movimentos oculares

Os dois sistemas de eixos são convenientes para a representação de deslocamentos apresentados pelo olho. Movimentos dele todo relativamente à origem do sistema orbitário de planos e eixos, isto é, movimentos oculares ao longo dos eixos orbitários (ou em quaisquer direções entre eles) são rotulados como translações. Movimentos do olho em torno de um de seus pontos, então considerado fixo, são denominados rotações.

Parece, portanto, simples admitir-se que um dos sistemas referenciais, o orbitário servisse para a definição de translações oculares, enquanto o sistema referencial ocular fosse usado para a definição das rotações do olho. Entretanto, ambos podem ser usados para esta última finalidade, o que acarreta novas complicações.

1) Translações

As translações são movimentos de pequena amplitude, pela própria condição de "acolchoamento" do bulbo ocular pelo conteúdo orbitário que o circunda, a lhe produzir uma certa fixidez, favorável aos movimentos rotacionais. Deslocamentos translacionais verticais (ao longo dos eixos SI) relativamente amplos, como os de um descenso ocular causado, por exemplo, por uma fratura de assoalho da órbita, chegando a 15 mm (mais do que o raio de curvatura normal do bulbo ocular) corresponde, para um objeto a 5 metros, a um estrabismo vertical de apenas 0,17º; para 30 cm de distância, esse desvio seria maior (2,86º) mas, ainda assim, considerado pequeno em termos rotacionais.

Quanto a translações ao longo dos eixos transversais (LM), quanto maiores as distâncias entre os centros de rotações oculares (identificadas, na prática, às distâncias entre os centros das pupilas, isto é à distância interpupilar) maiores os esforços de convergência para um dado ponto de atenção visual. (A um ponto simetricamente situado em relação aos centros de rotações oculares e a 30 cm da linha que os une, a convergência é de 9,53º para uma separação interpupilar de 50 mm e 13,31º para uma de 70 mm, praticamente um grau de variação da convergência requerida a cada variação de 5 mm na distância interpupilar).

Finalmente, o efeito de translações ao longo dos eixos longitudinais (AP) seria, tão somente, o de produzir rotações levemente assimétricas para objetos simetricamente dispostos relativamente aos olhos (além, obviamente, de alterações fisionômicas e de pequeníssimas mudanças da acomodação). Para uma distância interpupilar de 60 mm, a convergência simétrica a um objeto situado a 30 cm à frente da linha entre os centros de rotações oculares é de 11,42º, mas se um dos olhos sofresse uma protrusão de 15 mm, ela passaria a 11,72º (equivalente à de uma pessoa com separação de 61,58 mm entre os centros de rotações oculares). Essa diferença é praticamente negligenciável, mas, por outro lado, pode-se supor que a assimetria posicional dos olhos produzida por tal translação suscitasse a necessidade de um giro compensatório da cabeça (da linha ED' à E₂D", Figura 11 c). Então, a rotação de cabeça (para a direita, para retroceder o olho protruso e avançar o normal, conforme mostra a Figura 11 c), seria igual a arctan (p/i), em que p é a translação ao longo do eixo longitudinal e i a distância interpupilar; no caso, arctan (15/60) = 14,04º: um efeito de cerca de 1º de rotação compensatória da cabeça para cada milímetro de protrusão, ou de retração ocular!

2) Rotações

Como já adiantado, rotações oculares ocorrem em torno de um ponto do olho aproximadamente fixo em relação às paredes orbitárias. Entretanto, elas, podem ser, também, consideradas como referidas a um ponto absolutamente fixo na órbita (o da origem do sistema orbitário). Aparentemente, tratar-se-ia de um mesmo ponto, mas na verdade eles correspondem às origens de dois sistemas de coordenadas distintos (o do sistema ocular e o do sistema orbitário). Por outro lado, posto que os dois sistemas de coordenadas podem ser efetivamente coincidentes em suas respectivas origens, pareceria a princípio, indiferente que essa consideração fosse necessária.

No entanto, rotações consideradas relativamente a um sistema de coordenadas com eixos e planos fixos (o orbitário) são bem diferentes das consideradas relativamente a um sistema de coordenadas com eixos e planos móveis (o ocular), para essas mesmas rotações (Figuras 12 e 13)⁽⁸⁾. Em decorrência disso e desde que as observações nesses dois sistemas podem ser independentemente consideradas em cada um dos três planos fundamentais (as horizontais, no plano horizontal, orbitário, H, ou ocular, h; as verticais, no plano sagital, orbitário, V, ou ocular, v; e as torcionais, no plano frontal, orbitário, T, ou ocular, t), resultam oito possíveis combinações para arbitrar como seriam definidas as rotações oculares, isto é oito modalidades ou sistemas de coordenadas angulares, independentes (Tabela I).

 

 

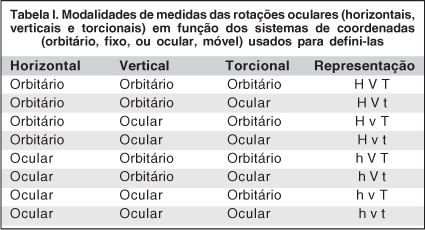
É claro que a partir de um desses sistemas de coordenadas pode-se chegar a outro, por conversibilidade dos respectivos valores. Mas é importante ressaltar que não há o menor sentido em se mencionar "um desvio angular de 15º no plano vertical e de 30º no horizontal" sem que se defina com quais dos critérios essas medidas são definidas. A figura 14 mostra que para coordenadas verticais e horizontais de idênticos valores, quatro diferentes pontos podem ser alcançados, dependendo dos sistemas referenciais escolhidos; ou que, inversamente, um dado ponto na superfície de uma esfera (ou, equivalentemente, no espaço) pode ser representado por quatro diferentes conjuntos de coordenadas angulares (Figura 15).

 

 

Mas, ainda mais perturbador, é o fato de que para cada um desses sistemas de coordenadas, o resultado final dessas rotações depende da ordem com que elas sejam consideradas!

Uma demonstração prática dessa condição é a do arranjo de prismas para a medida simultânea de componentes horizontal e vertical de um estrabismo. Pode-se superpor o prisma para a avaliação vertical sobre o da avaliação horizontal, mais próximo ao olho, ou vice-versa. No primeiro caso, é como se se fizesse inicialmente a rotação ocular no plano horizontal (A a H, Figura 14) e, a partir daí (ponto H, Figura 14) se procedesse à rotação ocular no plano vertical que passa pelo centro de rotação ocular (C), isto é, num meridiano vertical, para o trajeto H a F. No segundo caso, a primeira medida é a vertical (A a V) e a segunda a horizontal (V a E, Figura 14). Embora com relações simétricas, elas são "invertidas" (conforme a ordem de associação), originando os sistemas de Fick (ponto final F) e de Helmholtz (ponto final E), obviamente com significados diferentes.

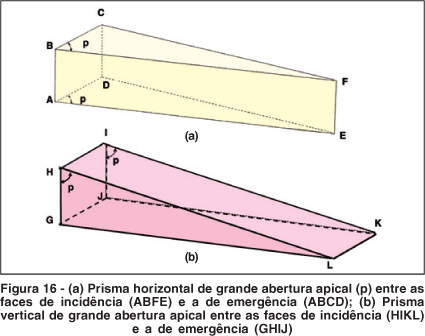
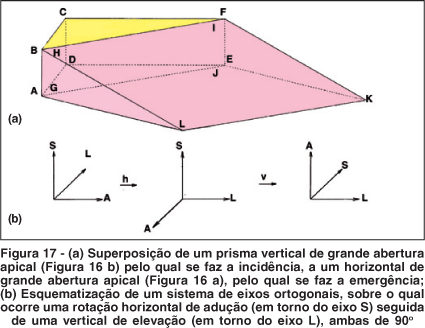
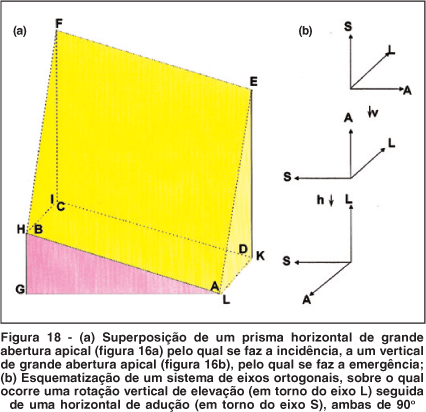
Com prismas de valores relativamente baixos essa diferença pode até passar despercebida. Mas a figura 16 é a de prismas de aberturas apicais muito grandes, para facilitar o entendimento de como o resultado final se torna completamente distinto se for o vertical que se superpõe ao horizontal (Figura 17), ou o inverso (Figura 18). Nessas figuras esquematiza-se, também, a posição dos eixos vertical (S), transversal (L) e longitudinal (A) na posição primária do olhar e após uma rotação horizontal de 90º (em torno de S) seguida de uma vertical de 90º (em torno de L), isto é, a do sistema de Fick (ponto F, Figura 14), ou com ordem invertida, a do sistema de Helmholtz (ponto E, Figura 14).

 

 

 

 

 

 

Na verdade, quaisquer dos pontos da figura 14 podem ser alcançados independentemente da ordem cronológica em que as rotações forem executadas. Por exemplo, pode-se chegar a F a partir de A fazendo-se primeiro uma rotação horizontal (de A a H), seguida de uma vertical (de H a F); ou, ao contrário, fazendo-se inicialmente a vertical (de A a V) e depois a horizontal (de V a F); ou, ainda, enfim, por qualquer outro trajeto (por exemplo, de A a F, em caminho "direto"). Por outro lado, a representação analítica das rotações, por equações, pode ser feita em modelo matricial, permitindo-se chegar ao resultado final de uma combinação de variáveis pelo produto das respectivas matrizes⁽⁸⁾. Ora, o produto matricial não é comutativo e depende da ordem em que ele é estabelecido. Ou seja, é importante, sim, a ordem em que as matrizes rotacionais forem consideradas em seus produtos, embora isso não signifique a ordem cronológica das rotações em sua concretude.

O que se relaciona ao produto matricial é um conjunto de critérios pelos quais são caracterizadas as rotações oculares. Por exemplo, as coordenadas de um ponto no sistema de Fick (ponto F, Figura 14) são definidas por uma rotação horizontal em torno de um eixo fixo (orbitário) e uma vertical em torno de um eixo ocular (móvel). No caso do sistema de Helmholtz prevalece o contrário: a rotação horizontal é medida em torno do eixo vertical ocular (móvel) e a vertical em torno de um eixo transversal orbitário (fixo). Em função desses critérios, vê-se que a ordem cronológica das rotações não tem importância (Figura 19). O aparente paradoxo de que o resultado das rotações horizontal e vertical possa depender da ordem cronológica de suas realizações (Figuras 17 b e 18 b) deve-se a que, naqueles casos, elas foram sempre consideradas como ocorrendo em torno de eixos oculares (móveis) (Figuras 19 b e c).

Ora, havendo seis permutações possíveis em cada uma das oito combinações de sistemas de coordenadas, ocorrerão, teoricamente, 6 x 8 = 48 diferentes possibilidades de se definir as rotações oculares, segundo o sistema de coordenadas escolhido para cada uma delas e a eventual "ordem" em que as rotações forem consideradas (Tabela II).

 

 

De qualquer modo, as 48 modalidades de consideração resultantes das diversas combinações entre, de um lado, os critérios utilizados para a definição das rotações oculares e coordenadas de suas medidas angulares em cada um dos três planos fundamentais; e, do outro, as formas analíticas de apresentação de suas relações (produtos matriciais, cujos resultados não são comutativos, mas dependentes da ordem desses produtos) (Tabela II), podem ser agrupados em seis sistemas distintos⁽⁸⁾ (Tabela III, Figuras 20 e 21).

 

 

 

 

G) Assimetrias posicionais

Além da (idealizada) posição primária do olhar, e com exceção das posições binoculares de sursunversão (ou supraversão), de deorsunversão (ou infraversão) no olhar para o infinito (eixos visuais paralelos), e das de convergência simétrica (a qualquer ponto do plano sagital mediano entre os dois olhos e, ou órbitas), todas as demais circunstâncias de fixação binocular de um ponto devem ser consideradas assimétricas. Estritamente, também, as cicloduções homônimas (inciclovergência e exciclovergência) e as abduções de iguais valores em cada olho apresentam-se como posições oculares simétricas, embora não sejam teleologicamente previstas pela natureza (na binocularidade humana, não há finalidade em se dirigir os olhares, simultaneamente, a pontos diferentes do espaço), nem possam (provavelmente por essa razão), ser voluntariamente acionadas(⁵). A assimetria pode ser funcional, ou geométrica.

De fato, no caso da assimetria funcional, o que se configura é a discrepância de ação dos músculos oculares externos. Por exemplo, numa dextroversão pura (olhar para o infinito), os eixos visuais permanecem paralelos, mas um olho faz abdução e o outro adução.

As assimetrias geométricas correspondem a quaisquer posições do ponto de atenção visual (ou de observação dos olhos examinados) a distâncias finitas e diferentes para cada olho. Assim, por exemplo, pela figura 22, se ED=7 cm, DF= 60 cm, FP= 30 cm e OP=20 cm, vem, para a rotação horizontal do olho direito:

 

 

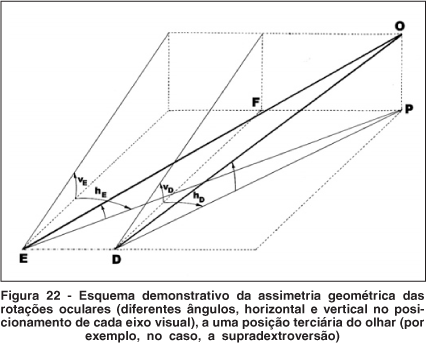
tan h_D = FP / FD = 30 / 60 → h_D = 26,57º

Para a rotação horizontal do olho esquerdo:

tan h_E = (FP + ED) / FD = (30 + 7) / 60 .^.. h_E = 31,66º

Para a rotação vertical do olho direito:

tan v_D = OP / PD = 20 / (30² + 60²)^1/2 .^.. v_D = 16,60º

Para a rotação vertical do olho esquerdo:

tan v_E = OP / EP = 20 / | (30 + 7)² + 60² | ^1/2 .^.. v_E = 15,84º

Ou seja, valores, todos, desiguais.

 

CARACTERIZAÇÃO DOS ESTRABISMOS: ASPECTOS OPERACIONAIS

A) Posição primária do olhar

1) Dificuldades para o estabelecimento temporal de coincidência dos eixos orbitários e oculares

A caracterização do conceito de posição primária do olhar já sofre a primeira contestação no aspecto temporal, isto é, quando se considera a quarta dimensão de nosso universo físico, o tempo. Como sabido, o olho não se mantém estático, mas sujeito a contínuos movimentos que, embora de dimensões relativamente reduzidas, são caóticos, de amplitude, direção e sentido irregularmente variáveis. Essa instabilidade dinâmica, frente ao pressuposto de coincidência espacial dos sistemas já contraria o princípio da recíproca simultaneidade temporal deles. Em outras palavras, a coincidência têmporo-espacial dos sistemas, cuja ocorrência é ocasional, aleatória, acidental e imprevisível, justifica a afirmação de que o postulado de posição primária do olhar é, em sua própria natureza, insustentável.

2) Dificuldades para referenciar externamente os sistemas orbitário e ocular

Deixando-se de lado essa primeira digressão sobre a casualidade com que o evento se torna possível e imaginando-se que a coincidência posicional dos eixos orbitários e oculares possa ser estável, a discussão seguinte é sobre como operacionalizá-la, isto é, com que modos e meios se alcance produzi-la. Com efeito, a questão da coincidência posicional dos sistemas orbitário (fixo) e ocular (móvel), já supõe um referencial (o sistema orbitário), todavia ainda insuficiente para materializar a posição primária do olhar, posto que ela se subordina a um novo elemento, o ponto de atenção visual, o objeto do "olhar". Em outros termos, a esse objeto material e, em particular, a seu ponto ao qual se dirige a atenção do "olhar", também cabe situá-los sobre um referencial independente e objetivo, as linhas "naturais" da horizontalidade e da verticalidade (linha gravitacional passando pelo ponto considerado).

Poder-se-ia pensar que, então, o referencial fixo passasse a ser o espacial, dispensando-se o orbitário, a quem substituiria. Movimentos oculares, como os de adução e abdução, inciclo e exciclodução, passariam a ser definidos em função de cada olho (por exemplo, a adução como olhar à esquerda pelo olho direito, abdução como olhar à direita, pelo olho direito, etc.) independentemente de um referencial orbitário. Entretanto, qualquer ponto do espaço poderia ser, alternativamente, definível como estando "em frente" do olho e, assim, perder-se a legitimidade referencial. Em síntese, tanto é importante o conhecimento da posição ocular como da orbitária, relativamente ao ponto de objetivação do olhar. Daí se falar em posição primária do olhar como a do olhar em frente (ao ponto objeto de atenção visual) com a cabeça ereta (referência do sistema orbitário relacionado ao eixo gravitacional), uma definição que, como já se viu, é, entretanto, insatisfatória.

3) Dificuldades para o estabelecimento posicional do sistema de eixos orbitários

No caso da órbita, seria possível estabelecer um eixo referencial horizontal (longitudinal ou transversal) e um vertical, segundo pontos convencionados arbitrariamente (linhas entre pontos considerados simétricos), ou por algum tipo de fundamentação (por exemplo, pela posição de canais semicirculares do labirinto). É claro que num exame clínico não se pode cogitar de referenciais escondidos da observação direta.

De qualquer modo, o correto posicionamento espacial da cabeça (eixos orbitários) exige a observação simultânea de (pelo menos) dois de seus planos, o que não é muito fácil. De fato, o exame do plano horizontal pode ser considerado dispensável, seja pela impossibilidade de se obter imagens a partir de baixo, seja pela costumeira inutilidade de imagens em vista superior (Figura 23).

Já as imagens do plano vertical sagital ("perfis", Figura 24) ajudam a referir possíveis inclinações relativamente ao plano horizontal (flexões ou extensões), mas não fornecem indícios para averiguação de como está a cabeça relativamente ao plano sagital (girada para a direita ou para a esquerda), ou ao plano frontal (inclinada para um dos ombros). As imagens do plano frontal ("face", Figura 25) auxiliam a discriminar tais inclinações e possíveis rotações relativamente ao plano sagital (para a direita ou para a esquerda), mas praticamente são inúteis para se aquilatar se a cabeça está flexionada ou estendida.

Por outro lado, a avaliação da posição da cabeça relativamente aos referenciais espaciais objetivos, para se poder chegar a defini-la como "normal" ou, alternativamente, "viciosa" (inclinada para um dos ombros, estendida ou flexionada, girada para a direita ou para a esquerda) é problemática, em função da bem conhecida variabilidade posicional dos acidentes anatômicos da face ou cabeça: linhas da face não são simétricas e, frequentemente, uma delas que possa ser eleita para coincidir com o plano horizontal (ou o vertical), não é paralela a outra, também servindo à mesma finalidade, nem ambas são perpendiculares a uma terceira, igualmente aproveitável para referenciar o plano vertical (ou o horizontal) da órbita (cabeça). Por exemplo, a linha entre os cantos externos, ou os internos, das pálpebras, pode discordar de outro padrão igualmente acessível, por exemplo, o das alturas das orelhas e, ou, não ser perpendicular a uma vertical utilizada como marcador (Figuras 26 e 27).

 

 

 

 

Em síntese, para conhecimento da posição do sistema tridimensional dos eixos orbitários:

a) não há boas perspectivas para a obtenção de referenciais no plano horizontal (Figura 23), isto é, por um exame por baixo da cabeça (virtualmente impossível) ou por cima (poucas probabilidades de aproveitamento).

b) Os exames dos planos frontal da cabeça (face) e sagital (perfil) são, portanto, ambos necessários.

c) Essa condição exige o possível ajustamento simultâneo de dois eixos (por exemplo, o vertical e o transversal) por técnicas especiais, como a provida por um jogo de espelhos para a observação das respectivas perspectivas normais (frontal e laterais). Ou, no caso mais simples, por um exame em perspectiva diédrica (frontal e sagital) que, de qualquer modo, supõe arbítrio (ajustamento pelo lado direito, ou esquerdo, do examinado).

d) A quase totalidade de acidentes anatômicos utilizáveis como supostamente simétricos para o arbitramento de linhas que possam ser tomadas como coincidentes ou paralelas a verticais, ou horizontais do espaço, oferecem-se, apenas, no exame frontal da cabeça (face).

e) A falta de transparência das estruturas da cabeça (ao exame visual do observador) não permite que os referenciais de um plano sejam vistos, em projeção, num outro plano. Por exemplo, a frontalidade do eixo transversal, estimado pela posição dos condutos auditivos, ou dos cantos palpebrais (laterais ou mediais) no exame frontal (da face) não pode ser confirmada pelo exame do plano horizontal (por cima da cabeça), nem por projeções do exame do plano sagital (perfil da cabeça).

f) Assimetrias faciais são comuns, não apenas inviabilizando padrões populacionais irretorquíveis como, principalmente, por gerar a desconformidade conflitante entre a possibilidade de um ajustamento (por exemplo, horizontal) e outro (por exemplo, vertical), pela ausência da hipotética perpendicularidade entre eles.

De qualquer modo, não é fácil discernir o que seja uma adequada posição da cabeça compatível com o conceito de horizontalidade e, ou verticalidade dos respectivos eixos orbitários, seja pelo exame do plano sagital (perfil, Figura 24), seja pelo do plano frontal (Figura 25).

4) Dificuldades para o estabelecimento posicional do sistema de eixos oculares

Sobre a determinação posicional dos eixos oculares, as dificuldades são de outra ordem. Por critérios objetivos o olho não oferece, externamente, por sua visão direta, não mais do que uma informação sobre seu direcionamento longitudinal (pelo eixo pupilar). Não há modo de se dizer por onde passa seu eixo vertical, nem seu transversal. O transversal, por exemplo, poderia ser arbitrado como passando pelos pontos mediais das inserções dos retos horizontais (uma proposta sobre a qual, provavelmente, ocorreriam fortes contestações, posto que as inserções esclerais dos músculos oculares externos não são uniformes e, ademais, dependentes das posições oculares e não seus padrões). De qualquer modo, mesmo então, seria difícil conhecer essas posições anatômicas durante um exame clínico.

Na retina, faltam elementos topográficos que possam caracterizar os eixos oculares horizontal e vertical. A oftalmoscopia possibilita a oportunidade de conhecer o seu "centro" (a fóvea), mas não seus eixos. O outro acidente eventualmente utilizável (o disco óptico) pode ser usado apenas como estimativa de torções oculares e, assim mesmo, de modo grosseiro. Enfim, não há como, objetivamente, operacionalizar-se a sistematização dos eixos oculares.

A única maneira conhecida de se "objetivar" linhas padrões (horizontais e, ou verticais) sobre a retina é pela técnica das pós-imagens. Mas esse procedimento depende da capacidade de informação da pessoa. Sobretudo, subjetivamente, as imagens percebidas são normalmente referidas como recíprocas das linhas do espaço. Para uma pessoa deitada de lado, uma linha horizontal continua a ser percebida como horizontal, embora se forme sobre o meridiano vertical da retina (sua pós-imagem será referida como vertical). Há, pois, dois tipos de informação possíveis, o cognitivo, empírico, que refere a verticalidade da linha pelo conhecimento prévio de que ela "é" vertical. E o da sensação retinotópica. Assim, por exemplo, se uma pessoa normal vê uma linha vertical, ela a refere como "vertical", mas essa informação de coincidência não pode ser tomada como fonte referencial para determinação da posição do eixo vertical da retina (e, pois, do olho). De fato, se ela inclina a cabeça para um dos lados (por exemplo, para a direita), ocorre um pequeno movimento torcional (de exciclotorção do olho esquerdo e de inciclotorção do direito) e embora a pessoa continue a referir a linha como "vertical", suas imagens não mais se formam sobre os meridianos verticais "verdadeiros" de cada olho. Por outro lado, para que a referência de que a pós-imagem dessa linha seja percebida como coincidente à vertical objetiva do espaço (sensação retinotópica), será preciso que o estímulo produzido tenha sido relacionado ao meridiano vertical da retina (e, portanto, represente o meridiano ocular vertical). Em outros termos, esse meridiano vertical já precisaria estar previamente na posição vertical, para que a 'caracterização" da verticalidade fosse possível... Consequentemente, um raciocínio circular, uma tautologia. Em síntese, o procedimento das pós-imagens:

a) Pressupõe que a pessoa esteja na posição primária do olhar para que a necessária estimulação sirva como padrão.

b) Pressupõe que, em seguida, a pessoa possa mencionar o que esteja percebendo, isto é, localizar (subjetivamente) a posição das pós-imagens relativamente ao referencial espacial objetivo.

Assim, tanto porque o teste requer, fundamentalmente, a resposta do sujeito examinado, ou seja, é subjetivo; quanto porque ele se mostre, essencialmente, tautológico (a resposta sensorial repete a atribuição dada ao estímulo) e redundante (exige-se a posição primária do olhar para se definir o que seja a posição primária do olhar), não se pode garantir qualquer "objetividade" ao seu uso.

Além disso, uma informação perceptual já é, por si mesma, um fator limitante dessa operacionalização, pois restrita a pessoas com boa capacidade de entendimento e de comunicação. De resto, nem mesmo a localização retinotópica de um estímulo garante que a respectiva percepção tenha reciprocidade com a realidade objetiva. Como argumento de sustentação da não fidedignidade das informações subjetivas como paradigmas da situação posicional do olho e, ou, do posicionamento de objetos no espaço (isto é, de suas "projeções" espaciais), lembre-se do estado de correspondência retínica (ou visual) anômala. Nele, a referência subjetiva gerada pelo estímulo retinotópico é completamente dissociada da que seria esperada.

5) Conclusão

Enfim, a coincidência dos eixos oculares (dos quais apenas o longitudinal é razoavelmente determinável) e orbitários (arbitrariamente asseverados, mas, geralmente, com proposições geométricas conflitantes) é de objetivação impossível e de consecução prática improvável. Na melhor das hipóteses consegue-se uma aproximação ao desejado (pelas incertezas quanto à objetivação de posicionamento do sistema orbitário) e, assim mesmo, apenas na dependência de informações (retinotópicas) pelo examinado.

Se não se pode, rigorosamente, pautar procedimentos que caracterizem tanto o sistema de eixos orbitários quanto o de eixos oculares, torna-se inviável afirmar sua coincidência; ou seja, torna-se impossível o conhecimento da posição primária do olhar, o ponto de partida para avaliações da oculomotricidade.

B) Quantificações

Um dos aspectos mais importantes em ciências da natureza diz respeito às medições. No caso dos estrabismos, as suas medições angulares, as das amplitudes de movimentos e outras, correlatas. Essas avaliações dependem de unidades e de técnicas empregadas. Esses aspectos serão criticamente examinados, objetivando ilações de aplicação prática.

1) Unidades de medição angular

Ângulos são classicamente medidos em graus de arco (º), ou seus submúltiplos, os minutos de arco (') e os segundos de arco ("). A variação dessas unidades é perfeitamente linear, ou aritmética, o que permite o uso de simples operações aritméticas para relacionar suas quantidades. Por exemplo:

30º = 3º x 10 = 5º x 6 = 6º x 5 = l5º x 2 = 14º + 16º = 13º + 17º = 32º - 2º = 90º/3, etc.

Um grau de arco (1º) é 1/360 da divisão angular de um círculo e, pois, o comprimento de seu arco é, também, 1/360 do comprimento da respectiva circunferência (1º=2 π R / 360) o que permite a relação entre a medida de um ângulo e a de um comprimento circularmente arqueado. Com exceção das medidas angulares muito pequenas já mencionadas, o minuto de arco (1º=60') e o segundo de arco (1'=60") são raramente usados nas medidas de estrabismos, ou de deslocamentos oculares, na prática clínica.

Outra medida angular também linear, ou aritmética é a do radiano, que equivale ao arco cujo comprimento é idêntico ao raio (R) da circunferência, ou seja R / 2 π R=1 / 2 π ≈ 0,159155 do perímetro. Como este equivale a 360º, 1 rad ≈ 57,296º. Visto que essa unidade é muito grande para a maioria dos propósitos dos atendimentos médicos dos estrabismos, propôs-se trabalhar, alternativamente, com um seu submúltiplo, equivalente à sua centésima parte, o centrad. Então:

1 centrad ≈ 0,57296º ≈ 34,38' ≈ 34' 22,65"

Mas embora essas unidades apresentem a vantagem de ser aritmeticamente operáveis, correspondem a medidas de comprimentos arqueados, de reprodução prática bem mais difícil que as de comprimentos retilíneos. Partindo-se então desse pressuposto, o de que seria mais apropriado medir ângulos cujas relações pudessem ser dispostas, ou conhecidas, de modos retilíneos, Prentice propôs trabalhar-se com a dioptria-prismática⁽⁹⁾, definida como a do ângulo compreendido pela distância de 1 cm à distância de 1 m do vértice do qual se mede o ângulo (Figura 28).

 

 

Isso permite confortabilíssimas ilações dimensionais. Por exemplo, para dois pontos separados por 60 cm em medida tomada a 3 m de distância de um deles, o ângulo em dioptrias-prismáticas é diretamente calculado por 60 (cm) / 3 (m)=20^Δ. Mas a conveniência dessa praticidade fica, por outro lado, comprometida pela desvantagem da perda das operações aritméticas com valores expressos por essa unidade. De fato, correspondendo a uma relação angular trigonométrica (tangencial), as quantificações em dioptrias-prismáticas passam a ser subordinadas a essa função. Afinal, o ângulo expresso em dioptrias-prismáticas (P) nada mais é do que cem vezes o valor da tangente do respectivo ângulo, em graus de arco. Pela figura 28:

P = BC (cm) / AB (m) = 100 BC / AB = 100 tan a

Por essa função trigonométrica, não se pode dizer, por exemplo, que 30^Δ seja o dobro de 15^Δ, nem que represente a metade de 60^Δ, ou que equivalha a 5^Δ + 25^Δ ou a 40^Δ - 10^Δ. Além do mais, todos os resultados dessas operações são, efetivamente, diferentes entre si (⁶):

15^Δ x 2 = 30,69^Δ

60^Δ / 2 = 27,70^Δ

25^Δ + 5^Δ = 30,38^Δ

40^Δ - 10^Δ = 28,85^Δ

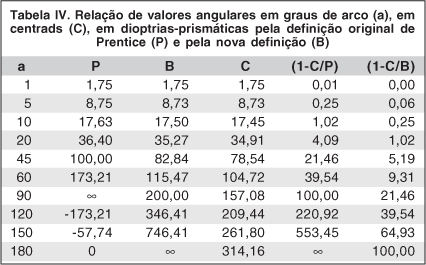
Essa não-linearidade na progressão dos valores expressos em dioptrias-prismáticas (P) conduz a resultados surpreendentemente perversos: ângulos de 90º equivalem a infinitas dioptrias-prismáticas; ângulos entre 90º e 180º são mostrados com valores negativos em dioptrias-prismáticas e, à medida que crescem nesse intervalo, os valores angulares nessa unidade tornam-se numericamente decrescentes. (Tabela IV).

 

 

Para se evitar essas impropriedades quantitativas, basta uma discreta modificação no conceito original de dioptria-prismática⁽¹⁰⁾, passando o ângulo dessa unidade (b) a ser compreendido pela separação de 1 centímetro entre dois pontos equidistantes do vértice e tomada perpendicularmente à distância de 1 metro (Figura 29). A metade desse ângulo (b/2) é definida em sua nova concepção pela relação 100 CM/MH= 100 BM/MH;

 

 

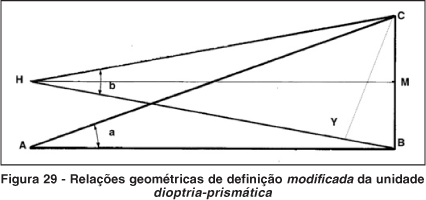
As vantagens das medidas por essa nova definição mostram-se por:

a) Os valores da unidade padrão tradicional (1^Δ=34' 22,579") e da nova (1^b=34' 22,631") são praticamente idênticos, variando apenas a partir da quinta casa decimal do grau de arco, ou da fração centesimal do segundo de arco:

1^Δ = 0,572938697º = 34' 22,579"

1^b = 0,572953020º = 34' 22,631"

Para se ter uma idéia linear dessa discrepância, a separação entre dois pontos do ângulo de 1^b a 5 metros é maior do que a de 1^Δ por uma diferença de apenas 1,25 μm! Assinale-se, também, que o valor do centrad é muito mais próximo do de 1^b do que do de 1^Δ (1 centrad=0,572957795º=34' 22,648"): ele é maior do que 1^b por apenas 0,0008%. A tabela IV mostra a relação de valores angulares nessas diferentes unidades e o erro da linearidade pelo uso da nova unidade (B) e da dioptria-prismática (P), quando comparados ao valor do centrad (C).

O erro de 5% com o valor de B é apenas alcançado para o ângulo de 44º 09' 35,75" ≈ 97,11^Δ, enquanto idêntico erro com a unidade dioptria-prismática já se atinge para valores a partir de 40,57^Δ. Ora, rotações oculares e desvios dessa magnitude são considerados como "extremos", na prática. Portanto, para a quase totalidade das aplicações clínicas, essa nova unidade poderia ser usada como de variação aritmética.

b) Por sua vez, a metade desse ângulo equivale a 100 y/2x=50 y/x em dioptrias-prismáticas. Assim, pode-se dizer que o ângulo B tem o dobro do valor angular (em graus de arco, ou em centrads) cuja metade (em graus de arco ou em centrads) é dada pela metade (em graus de arco ou em centrads) do valor de P. Em outras palavras, o dobro do ângulo de 10^Δ (≈ 5,711º), isto é 2 x 5,711=11,421º=20^b. Mas pelo fato de a relação angular entre P e a e entre 2a e B não ser linear, não se pode dizer que 2P=B. A relação entre essas duas variáveis pode ser geometricamente calculada:

P = tan b = HM / BM

HM = (2 x. y). (4 x² + y²)^-1/2

BM = (4 x² - y²). { 2 (4 x² + y²)^-1/2 }

Portanto:

P / 100 = (4 x. y) (4 x² - y²)^-1/2 .^.. P = 40000 B / (40000 - B²).

Ou, reciprocamente, B={- 100 ± (100² + P²)^1/2}. 200. P^-1

(O sinal negativo da raiz é empregado para os valores negativos de P).

c) Esse ângulo alcança valor infinito apenas para 180º. Entre 0º e 180º os valores dele são, sempre, positivos e crescentes.

2) Observação visual desarmada da menor rotação ocular

Um movimento rotacional do olho observado de 0,3º (= 0,52^Δ) equivale ao deslocamento retilíneo de um ponto em sua superfície de 64 μm (r=12,2 mm). Para um observador, cujo primeiro ponto nodal esteja a 30 cm desse ponto, isso equivale a um ângulo visual de 44", portanto pouco acima da máxima capacidade visual resolutiva de um olho, correspondendo a uma acuidade visual de 1,36. Já 100 μm correspondem a um ângulo visual do observador de 69", equivalente à acuidade visual 0,87. Se o olho do observador fosse absolutamente estável em sua fixação, e com a acuidade visual padronizada como normal, correspondente ao ângulo visual de 60", isso equivaleria a poder perceber na superfície do olho observado, 30 cm à frente, deslocamentos a partir de 87 μm, o que equivale a 0,41º ≈ 0,71^Δ.

Entretanto, posto que o olho do próprio observador também não permanece estável, mas igualmente sujeito às oscilações que desestabilizam a fixação visual, a detecção perceptual do "mínimo" movimento do olho observado passa a uma condição probabilística: pode, ou não, ser notado, nas circunstâncias supostas (por exemplo, se os dois olhos se deslocarem simultaneamente no mesmo sentido, ou com pequenas defasagens temporais e, ou, diferentes amplitudes). De fato, se valores de oscilação de até 28' forem contados em dobro (56'), isso equivale a 1,63^Δ. Daí se pode inferir que por essa capacidade de percepção de deslocamentos oculares pelo olho desarmado não se chegue a detectar desvios de ângulos menores, pela técnica de refixação a um "ponto" de atenção visual.

C) Métodos de medida do ângulo de estrabismo

O mais simples é o da avaliação desarmada das posições oculares e de suas relações, por observação direta, geralmente utilizado quando não há possibilidade de se fazer um estudo crítico das fixações oculares, por falta de condições de estabelecê-las (falta de colaboração, por exemplo, em crianças muito novas; falta de visão). O método de Hirschberg consiste em se observar a posição do reflexo de uma fonte luminosa pela córnea, referida relativamente ao centro da pupila.

Originalmente, a proposta admitia que quando o reflexo corneal da fonte luminosa, situada a 12 polegadas (30,48 cm), fosse percebido mais próximo do centro da pupila que de sua margem, o desvio equivaleria a 5 ou 6º. Se na margem pupilar (pupila de 3 mm), entre 12 e 15º; se na metade da distância dessa margem ao limbo, 25º; no limbo, 45 a 50º e além dele, 60 a 80º. Wheeler⁽¹¹⁾ estimou a relação entre o valor do ângulo do estrabismo e a leitura da descentração do reflexo como de 8º/mm. Apesar de simples e, por vezes, o único que se pode aplicar (crianças muito novas), esse método é, portanto, relativamente grosseiro. Mesmo que se consigam leituras com uma escala milimétrica e por interpolação, os erros de avaliação estariam, no mínimo, ao redor de 4º (cerca de 7^Δ) mas podem atingir 11º (ou seja, quase 20^Δ)⁽¹¹⁾.

1) Medidas pela fixação foveal

Como já visto, o direcionamento ocular a um ponto objeto do espaço não pode ser considerado com precisão maior do que 18' (=0,3º ≈ 0,52^Δ), uma indeterminação originada da relativa incapacidade de o examinado fazer um movimento voluntário dessa magnitude entre dois pontos separados por tal distância angular.

Outro aspecto limitante da precisão das chamadas medidas objetivas num exame clínico de rotina (sem métodos específicos de registro das rotações oculares como, por exemplo, o fotoelétrico) deriva do próprio examinador, por sua incapacidade de observar movimentos oculares muito delicados. Ou, pelo menos, detectá-los com o significado de desvios e não, simplesmente, de falhas ocasionais do mecanismo de fixação ocular. Tem sido referido que movimentos (corretivos da posição de fixação, ou não) de até cerca de 2^Δ não são comumente perceptíveis, mas que esse valor varia em função da experiência do examinador. De fato, 2^Δ ≈ 1,15º, o que corresponde a um deslocamento tangencial (num olho com raio de curvatura igual a 12,2 mm) de 244 μm. Ora, conhecendo-se a pouca nitidez de linhas demarcatórias referenciais na superfície do olho, não fica difícil a explicação da causa dessa insuficiência de precisão na semiologia. No caso do centro da pupila, o deslocamento da posição de um reflexo luminoso correspondente a esse ângulo é ainda menor, em torno de 170 μm.

Desde que se admita que erros de 2^Δ na avaliação de um desvio sejam clinicamente possíveis, o valor de 4^Δ entre duas avaliações de idêntica magnitude angular, uma (de 2^Δ) para mais, outra para menos, reforça a idéia de que diferenças dessa ordem de grandeza em medidas objetivas não podem ser interpretadas como possuindo significado clínico. Obviamente, um desvio de 4^Δ pode ser notado e ortotropia (0^Δ) também; mas nem sempre com facilidade, suscitando a conveniência de exames especiais. (Coincidentemente, o teste de Irvine⁽¹²⁾ popularizado por Jampolsky para o diagnóstico diferencial entre microestrabismo e heteroforias, usa um prisma de 4^Δ).

2) Medidas subjetivas

Nos exames subjetivos, maior rigor quantitativo pode ser obtido pela adequada informação do examinado, mas fatores de complicação se apresentam. Com efeito, diferenças posicionais entre os eixos visuais principais de até 0,5^Δ podem ser referidas (por exemplo, em exames como os com vidros estriados de Maddox). Mas para que essa medida seja confiável e aproveitada alguns requisitos serão necessários.

a) O primeiro, obviamente, é o da capacidade de a pessoa examinada informar corretamente sua percepção. Isso nem sempre é fácil, porque elementos supressivos da visão binocular podem tornar problemática, ou impossível, a noção sobre a posição simultânea das percepções visuais originadas de cada olho.

b) O segundo elemento de dificuldade é o do conhecimento de se a informação de um ângulo subjetivo diferente do ângulo objetivo medido nesse paciente é realmente diferente (o que corresponde ao diagnóstico de correspondência visual anômala), ou é igual (isto é, a correspondência visual é normal), mas a discrepância se deva à chamada dissociação fusional binocular. Realmente, desequilíbrios oculomotores podem se achar compensados no ato binocular, mas surgirem quando a fusão (binocular) for impedida, o que costuma ser um dos fundamentos do próprio exame. Ou seja, para se testar se há, ou não, desvio entre os eixos visuais, usam-se procedimentos que podem manifestá-lo. Quanto mais intensa for a chamada dissociação binocular, mais facilmente aparecem os desvios compensados (heteroforias) e com maior amplitude.

c) Além disso, o mecanismo fusional binocular admite uma discrepância posicional entre os eixos visuais de cada olho para o ponto objeto a ser visto, sem que isso implique estrabismo ou, mesmo, erro funcional. Pela área fusional de Panum, elementos retínicos que não são exatamente correspondentes (isto é, possuindo diferentes direções visuais de percepção do espaço) podem ser estimulados pela imagem de um mesmo ponto objeto do espaço, sem que este seja percebido com diplopia (em diferentes direções do espaço, como se deveria esperar), mas "fundidos". Nessa circunstância esse ponto é percebido como mais aproximado, ou distante, que outros, nas circunvizinhanças. A área fusional de Panum que permite a fusão cortical de imagens para elementos visuais não exatamente correspondentes, é de cerca de 15' no centro do campo visual, mas aumenta com a excentricidade. É curioso que os valores da área de Panum em torno do eixo visual principal sejam praticamente coincidentes aos da "imobilidade" ocular demonstrada para a mudança de fixação entre dois pontos com proximidades angulares como essa.

De qualquer modo, a própria medida da estereopsia corresponde a desigualdades no posicionamento binocular ao objeto a ser fixado. Assim, ao se falar sobre uma estereopsia de 3000" (= 50' ≈ 0,83º ≈ 1,45^Δ) admite-se a existência desse desvio entre os eixos visuais.

3) Medidas com prismas

Pelo progressivo desestímulo ao uso de aparelhos (como o sinoptóforo) para a medida angular dos estrabismos, passou-se ao dos prismas. Esses artefatos ópticos trazem o benefício de menores custos para as suas aquisições, portabilidade e eficiência nos propósitos para os quais são empregados. Em contrapartida, carreiam uma apreciável série de cuidados a serem tomados^(13-14), tais como os de que:

a) Os valores com que os prismas são assinalados dependem de critérios de definição e se aplicam para a respectiva condição específica, isto é, para uma determinada direção de incidência da luz sobre eles; esses critérios podem variar conforme o fabricante (Figura 30, prismas de 40^Δ conforme a definição pela chamada posição de Prentice, em "a", ou pela do desvio mínimo, em "h").

b) Reciprocamente, o modo como o prisma é anteposto ao olho, isto é, a inclinação de suas faces anguladas relativamente ao plano frontal da cabeça, influi no resultado da medição (Figura 30, posições "a", "b", "c", "d", para o prisma de 40^Δ definido pela posição de Prentice; e posições "e", "f", "g", "h", para o definido pela posição do desvio mínimo).

c) A posição de desvio mínimo pela qual cada prisma deve ter seu respectivo valor padronizado (Figura 30 h) é de difícil reprodução prática.

d) Os distanciamentos do objeto de fixação ao prisma e do prisma ao olho, assim como o posicionamento do objeto relativamente ao que seria a posição primária do olho, interferem nos resultados das medições angulares obtidas.

e) Finalmente, todos esses fatores dependem do material com que o prisma for confeccionado; isto é, padronizações aplicáveis a prismas de mesmos valores, mas com diferentes índices de refração de seu material de construção, não são, reciprocamente, intercambiáveis.

Em verdade, o valor atribuído a um prisma, ou seja, aquele com o qual ele é apresentado, depende do índice de refração do material com que ele é confeccionado (n₂), da angulação entre suas faces de incidência e refringência (p) e do critério, arbitrário, utilizado pelo fabricante para essa quantificação, isto é, da inclinação da luz incidente (i₁) com a qual esse valor atribuído (P) é estabelecido. Para outra posição de uso, isto é, para uma determinada inclinação de uma das faces relativamente ao objeto (a face anterior) ou ao olho (a posterior, por exemplo, w), o desvio produzido pelo prisma (Δ) é diferente do rotulado (P). Finalmente, na dependência da distância entre o objeto e o centro de rotação ocular (d) e da distância deste ao prisma (q), o efeito rotacional produzido (β) - que, afinal, é o que em última análise interessa - corresponde a novos cálculos a serem feitos⁽¹⁴⁾.

Em síntese, o resultado de um prisma como instrumento de medida de um estrabismo depende de múltiplas variáveis. É surpreendente, entretanto, que essa condição de variabilidade de efeitos não seja geralmente considerada e que o valor de um prisma diante do olho permaneça, para quaisquer posições do objeto (e, ou, desvios do olho) sempre tomado como único, constante, igual ao que o fabricante lhe atribui (P). As tabelas V e VI e as figuras 30 e 31 exemplificam algumas dessas circunstâncias de prismas e as respectivas variações dos efeitos rotacionais (β) produzidos. (As tabelas V e VI foram construídas com base nos seguintes parâmetros: índice de refração do material do prisma, n₂=1,49; distância do centro de rotação ocular ao objeto de fixação, d=33 cm; distância do centro de rotação ocular ao prisma, q=3 cm.)

 

 

 

 

 

 

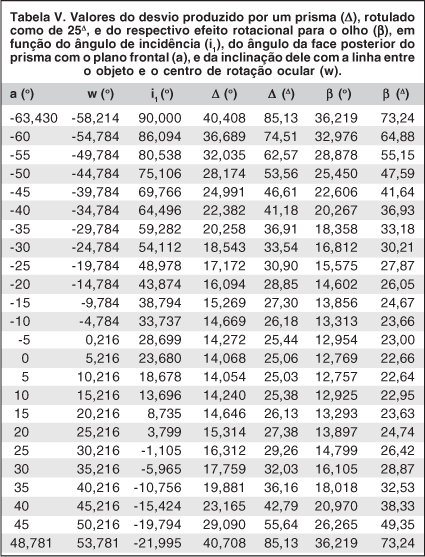
Contudo, esses fatores de variação dos poderes dos prismas e de seus efeitos não são completamente restritivos ao emprego desses artefatos. Por exemplo, a tabela V representa cálculos para um prisma de acrílico (n₂=1,49), padronizado como de 25^Δ pelo critério do desvio mínimo, portanto com abertura apical p=27,597º, com distância do centro de rotação ocular ao ponto de desvio (q) e ao objeto de fixação (d) de, respectivamente, 3 e 33 cm. Nessas condições, para inclinações relativamente amplas ao objeto de fixação (a entre +25º e -20º) e, consequentemente, para as respectivas inclinações da incidência (i₁ entre -1,1º e 43,9º), os efeitos prismáticos observados (β) apresentam variação inferior a 2^Δ relativamente a um valor em torno de 24,5^Δ, isto é, conservam-se praticamente constantes. Claro que para prismas de maiores valores, as condições mostram-se mais críticas. Na tabela VI, por exemplo, as variações entre -5º e +10º e entre +10º e +20º (portanto intervalo menor) chegam, aproximadamente a 3,5^Δ (variação maior).

4) Conclusão

De qualquer modo, por se renunciar à determinação do que seja o marco "zero" para as medidas do posicionamento ocular, não faz muito sentido a referência a exatidões quantitativas sobre elas em outras situações do espaço e a um extremado rigor nessas considerações. Somam-se a isso as múltiplas variáveis influentes nos principais métodos de medida utilizados para essas quantificações e as dificuldades operacionais para controlá-las.

Além disso, pequenos desequilíbrios da oculomotricidade deixam de ser consideráveis:

a) Pela autocompensação, assintomática, por mecanismos fusionais, na contingência de uma visão binocular normal;

b) Pela não aparência de inadequação posicional (estrabismo), quando os mecanismos fusionais não são garantidos; ou

c) Pela impossibilidade de tratá-los adequadamente nos casos de visão binocular anômala.

D) Lentes e seus efeitos

Outra condição de grande importância na quantificação dos desvios angulares dos estrabismos é a referente ao efeito das lentes convencionais. Agora, entretanto, não se tratará do tema das alterações convergenciais por elas produzidas, isto é, das decorrentes das mudanças da acomodação: reduções (desejadas) de esodesvios, ou aumentos (indesejados) de exodesvios relacionados à diminuição da convergência binocular, induzida pela redução da acomodação (pela prescrição de lentes positivas); ou, ao contrário, aumento de esodesvios (indesejado) ou redução de exodesvios (desejada), relacionados ao aumento da convergência, suscitada pelo aumento da acomodação (por prescrição de lentes negativas, ou redução de positivas). Essas mudanças são dependentes da sincinesia entre a acomodação e a convergência e expressas pela relação C_A / A (convergência "acomodativa" induzida pela acomodação ou, simplesmente, por seu estímulo). Mas, especificamente, serão abordadas as variações dos efeitos dessas lentes em relação aos que costumam ser delas esperados.

De fato, não é correto admitir-se que a acomodação (A) suscitada pela fixação de um dado objeto, situado adiante do primeiro plano principal do olho dependa apenas da distância (medida em metros) entre esses dois pontos (y, ou da sua respectiva recíproca, M=1/y), do valor da eventual ametropia (V) e da lente eventualmente usada (L), conforme a fórmula simplificada:

A = (1/y) + V - L = M + V - L

Para que o valor correto da acomodação seja calculado, deve também entrar em consideração a medida da distância vértice (s). Ela vai do segundo plano principal (ou imagem) da lente (frequentemente tomado como coincidente à sua superfície posterior) ao primeiro plano (ou objeto) do olho (frequentemente tomado como coincidente à superfície anterior da córnea), o que transforma a fórmula a⁽¹⁵⁾:

A - V = { M - L (1 - s.M) } {1 - s.L (1 - s.M)}^-1

O próprio vício de refração (V) costuma ser apresentado com o valor da lente convencional com o qual ele se corrige (L₀), o que também depende da distância vértice:

L = L₀ / (1 - s.L₀)

Por outro lado, quando um objeto é visto através de uma lente (L ou L₀) sem que o eixo visual passe pelo centro óptico dessa lente, ela atua como um prisma, cujo efeito (P, em dioptrias-prismáticas) é proporcional à respectiva descentração (d, com valor dado em centímetros):

P = L. d

Ora, a descentração (d) com que o eixo visual se afasta do centro óptico da lente é função da distância vértice (s), da distância ao objeto fixado (y) e da distância interpupilar do examinado (i) (Figura 32):

i / 2y = d / (s + r)

 

 

 

Em razão disso, haverá prismação (suscitando a detecção artificial de um desvio, quando ele não houver; ou modificando seu valor, se ele existir, para mais, ou para menos - podendo até invertê-lo) quando forem usadas lentes:

a) Em lateroversões, mesmo quando as lentes forem iguais, por prismações diferentes, pela desigualdade entre as incidências, quando o objeto estiver a distâncias finitas (Figura 33 a), ou em convergências assimétricas (Figura 33 c).

b) Em casos de anisometropias (Figura 33 d).

De fato, pela figura 33 a, para o olho esquerdo d_E/(s + r) = (i + x)/y e para o direito d_D/(s + r) = x/y. Portanto:

P_E - P_D = L_E.d_E - L_D. d_D = L_E {(i + x)(s + r)/y} - L_D { x (s + r)/y }

∴ (P_E - P_D). y / (s + r) = x(L_E - L_D) + i. L_E

Por exemplo, para i=6 cm, y=36 cm, x=30 cm (angulação de 45º para o olho em adução e de 39,8º para o em abdução). s=1,5 cm e r=1,22 cm, vem:

P_E - P_D = 2,267 (L_E - L_D) + 0,453 L_E = 2,72 L_E - 2.267 L_D

Assim, mesmo que L_D=L_E, ocorrerá prismação (P_D - P_E ≠ 0) em função dos valores das lentes (no caso L_D=L_E), r, s, i, x e y. Nesse exemplo, resulta que se L_D=L_E=8 D, então ΔP=3,63^Δ. Note-se que o sinal negativo para a apuração do efeito prismático (isto é, P_D - P_E) decorre de que lentes de mesmo sinal correspondem, nessa condição (lateroversão), a prismas de sinais diferentes. Por exemplo, no caso da figura 33 (lentes positivas), prisma de base temporal para o olho que aduz (esquerdo) e de base nasal para o que abduz (direito).

Em convergência, simétrica (Figura 33 b) ou assimétrica (Figura 33 c), as descentrações serão, para o olho esquerdo, d_E/(s + r) = x/y; e, para o direito, d_D/(s + r) = (i - x)/y. Ou, sendo a o valor da assimetria da convergência, isto é, x = (i/2) - a, o efeito prismático (ΔP) será, agora, dado pela soma (pois lentes de sinal idêntico acarretarão efeitos prismáticos também de mesmo sinal):

P_E + P_D = ΔP = L_E.d_E + L_D.d_D = L_E {(s + r). x / y} + L_D {(s + r) (i - x) / y} .^.. ΔP. y / (s + r) = L_E. x + (i - x) L_D = x (L_E - L_D) + i. L_D

Se as lentes forem de valores iguais (L_D = L_E = L):

ΔP. y / (s + r) = i. L = 2 (a + x). L

Para L_E = L_D = + 8, s = 1,5 cm, r = 1,22 cm e y = 36 cm, ΔP = 3,63^Δ.

Se as lentes forem positivas, o efeito prismático é de base temporal, o que faz com que a convergência seja suscitada, ou esodesvios sejam compensados. Se as lentes forem negativas, o efeito prismático será de base nasal, o que faz com que a convergência seja aliviada (reduzida), ou exodesvios sejam compensados. Ora, sobre a acomodação, lentes positivas e negativas produzirão, respectivamente, valores menores e maiores o que, de certo modo, significa um efeito dissociado: as positivas suscitando menor acomodação, mas maior convergência e as negativas suscitando maior acomodação, mas menor convergência. Ou, por outras palavras, nas lentes positivas a menor convergência induzida pela menor acomodação suscitada é contrabalançada por maior convergência suscitada pela prismação de base temporal, para perto; enquanto, para as lentes negativas, a maior convergência, suscitada pela maior acomodação é contrabalançada pela menor convergência requerida pela prismação de base nasal, no olhar para perto.

Na comparação com as lentes de contato, as convencionais positivas produzirão, para perto, maior acomodação e, pois, maior convergência, mas esta, de certo modo é compensada pela prismação de base temporal. Com as convencionais negativas dá-se o oposto: nas fixações para perto há menor acomodação e, pois, menor convergência, também compensada pela prismação de base nasal. Uma interessante "auto-compensação", o que torna, teoricamente, em termos de relação entre a acomodação e a convergência, as lentes convencionais tão "equilibradas" quanto as de contato. (Com estas a acomodação a uma determinada distância é a "normal", isto é, sem as variações induzidas pela distância vértice; e, também, não há prismação.) Obviamente, os efeitos "dióptricos" (acomodativos) sobre a convergência serão regidos pelo valor da relação C_A/A, enquanto os "prismáticos" dependerão das variáveis supramencionadas, e de suas relações.

c) Em casos de anisometropia, em quaisquer direções do olhar ocorrerão diferenças de posicionamentos oculares (desvios, compensados, ou não, induzidos pelas respectivas prismações diferentes), com eventual diplopia. Por exemplo, se houver no olho esquerdo uma lente com valor mais positivo (ou menos negativo) que a do olho direito, manifestar-se-á:

i) em dextroversão, exotropia (com diplopia cruzada) pela maior prismação de base temporal no OE (no caso de lentes positivas) ou no OD (no caso de lentes negativas) (Figura 33 d);

ii) em levoversão, esotropia (com diplopia homônima), pela maior prismação de base nasal no OE (no caso de lentes positivas), ou no OD (em caso de lentes negativas);

iii) em infraversão, desvio vertical E/D, pela maior prismação de base superior no OE (em caso de lentes positivas) ou de base inferior no OD (em caso de lentes negativas);

iv) em supraversão, desvio vertical D/E, pela maior prismação de base inferior no OE (em caso de lentes positivas) ou de base superior no OD (em caso de lentes negativas).

Assim, desvios artificialmente produzidos podem ser detectados, com incomitâncias incomuns (como a acima descrita) e, ou, desvios reais aparecerem, super ou subestimados, com incomitâncias aumentadas ou diminuídas, conforme o caso de associação. Por exemplo, para L_D = - 8 D e L_E = - 2 D, com os parâmetros de x, y, i, s, e r já enunciados (respectivamente 30 cm, 36 cm, 6 cm, 1,5 cm e 1,22 cm), encontrar-se-á, em dextroversão, um exodesvio de -9,97^Δ, em levoversão um esodesvio de +17,23^Δ, em infraversão e em supraversão (ângulo de 45º, equivalente a x/y, portanto d_E = d_D = s + r), respectivamente um desvio vertical E/D de 16,32^Δ e um desvio vertical D/E de 16,32^Δ, simulando uma contenção rotacional do olho esquerdo, tanto no plano horizontal quanto no vertical!

 

CONCLUSÕES FINAIS

1) Não há uma definição estabelecida, uniforme e consistente sobre o termo "estrabismo". A multidiversidade das alternativas deriva das várias condições pelas quais eles se manifestam, nem sempre em associação, e que correspondem a seus diferentes estados. Assim, pela concepção do estrabismo como uma afecção do estado oculomotor valoriza-se a diferença do posicionamento binocular, assumida pelo exame do direcionamento dos eixos visuais de cada olho na fixação a um objeto de atenção visual. Mas a operação pela qual se pode estabelecer a diferença entre normalidade e estrabismo depende, precisamente, da capacidade de colaboração do examinado para a determinação "objetiva" daqueles direcionamentos e, pois, resulta de múltiplos fatores. Por exemplo, da integridade das funções sensoriais visuais (afetadas por lesões da retina, nervo óptico, vias visuais e córtex occipital), da estabilidade da fixação visual e de seus comandos (comprometida em nistagmos e em apraxias) e da própria intenção de participação no exame (em falta em crianças, e em estados mentais deficientes, ou aversivos). Por outro lado, com fundamento no estado sensorial com que se dá a percepção do espaço pelo examinado, define-se um ângulo subjetivo para o estrabismo, de cuja comparação com a medida objetiva resulta o conhecimento da chamada correspondência visual (ou retínica), normal ou anômala. Intrinsecamente, a determinação dessa importante característica funcional dos estrabismos é radicada na informação do examinado e que, além de sua necessária volição e capacidade de colaboração, depende de mecanismos de adaptação ao estado de desvio dos eixos visuais (supressões da percepção da imagem do objeto de atenção visual formada por um dos olhos) dos quais a própria correspondência visual é consequência. Finalmente, o estado fisionômico pelo qual também se pode caracterizar um estrabismo por sua aparência, tem por base um outro fator, o direcionamento dos eixos pupilares, comumente bem diferente do direcionamento dos eixos visuais.

2) O posicionamento binocular, objetivo, ou aparente, é relativo ao ponto de observação, ou ao ponto para o qual a atenção visual é dirigida. Assim, é freqüentemente impossível a afirmação sobre se há ou não estrabismo, ou qual a qualidade de seu desvio, ou sua magnitude pelo exame de uma fotografia, por exemplo (⁷).

3) A posição primária do olhar pode ser, em princípio, concebida como a de coincidência de eixos homônimos dos sistemas orbital (fixo) e ocular (móvel), assumidos para as medidas de ângulos dos estrabismos e de movimentos oculares. Mas, estritamente, requer ainda, para sua completude, a referência a eixos corporais e ao gravitacional terrestre. De qualquer modo, essa posição seria apenas transitoriamente obtida e assim mesmo como casual, pela instabilidade natural do próprio olho. Além disso, as condições de seu estabelecimento não são reprodutíveis, de um lado pelas dificuldades de conhecimento de referenciais objetivos para os eixos oculares e de outro pelas assimetrias entre os possíveis (e arbitrários) parâmetros anatômicos de posicionamento da órbita no espaço. Assim, chega-se à conclusão de se tornar impossível a materialização do conceito sobre o ponto zero do sistema oculomotor, ou seja, daquele de onde começar medidas.

4) Não há padronização, nem consenso, sobre em qual dos possíveis sistemas referenciais de medidas para os três planos fundamentais do espaço elas devam ser consideradas. Menções a valores angulares de rotações, ou de desvios combinados (por exemplo, horizontal e vertical) sem a do referencial em que se faz a sistematização tornam-se, portanto, desprovidas de significado.

5) Com exceção de direcionamentos a posições sobre o plano sagital mediano entre os sistemas referenciais relativos aos olhos direito e esquerdo, todos os demais correspondem a situações de assimetrias rotacionais. Por exemplo, numa dextroversão pura (no plano horizontal) um olho faz abdução, enquanto o outro faz adução.

6) O critério com que os direcionamentos oculares no espaço são estipulados admite uma imprecisão em torno do valor da unidade com que são comumente apresentados e, em certas situações, maior que ela. Isso torna impróprio o uso de valores fracionários das medidas apresentadas.

7) A unidade consagrada de medidas de estrabismos (dioptria-prismática), embora oferecendo algumas vantagens práticas (relações diretas entre medidas lineares) não se ajusta a tratamentos aritméticos (o que exige correções, mesmo em suas operações mais simples) e alcança valores impraticáveis em desvios muito grandes (infinitas dioptrias-prismáticas para 90º, valores negativos e numericamente decrescentes entre 90º e 180º).

8) Artefatos rotineiramente usados para quantificações angulares (prismas) têm valores dependentes de múltiplas variáveis, dificultando correções sobre as respectivas leituras.

9) A superposição de prismas nas quantificações "independentes" em planos ortogonais (o horizontal para a incidência e o vertical para a emergência, ou vice-versa) não é indiferente, mas condicionada ao sistema arbitrado para as medições.

10) Avaliações da medida angular de um estrabismo são também influenciadas pelos efeitos prismáticos de lentes convencionais diante dos olhos da pessoa examinada (em suas possíveis descentrações, ou em posições secundárias ou terciárias do olhar nas lentes centradas).

 

REFERÊNCIAS

1. Perea J. Estrabismos. 2ª ed. Toledo: Artes Gráficas; 2008. cap. Definiciones de "estrabismo" a lo largo de la historia.         

2. Gullstrand A. Appendices to part I. In: Southall JPC, editor. Helmholtz's treatise on physiological optics. Rochester: The Optical Society of America; 1924. p.352.         

3. Alpern M. Specification of the direction of regard. In: Davson H, editor. The eye. 2^nd ed. New York: Academic Press; 1969. p.5-12. vol. 3 Muscular mechanisms.         

4. Sears FW. Física: Óptica. Rio de Janeiro: Livro Técnico, 1964. vol. 3.         

5. Fincham WHA. Optics. 7th ed. London: Hatton Press; 1965.         

6. Alpern M. Types of movement. In: Davson H, editor. The eye. 2^nd ed. New York: Academic Press; 1969. p.65-174. Vol 3: Muscular mechanisms.         

7. Rashbass C. The relationship between saccadic and smooth tracking eye movements. J Physiol. 1961;159:326-38.         

8. Bicas HEA. Estudos da mecânica ocular. I. Sistemas de definição das rotações oculares. Arq Bras Oftalmol. 1981;44(1):18-25.         

9. Prentice CF. A metric system of numbering and measuring prisms. Arch Ophthalmol. 1890;19:64-75;128-35.         

10. Bicas HEA. Unidades de medidas. In: Bicas HEA, Souza-Dias H, Almeida H, editores. Estrabismos. Rio de Janeiro: Cultura Médica; 2007. p.69-72.         

11. Wheeler MC. Objective strabismometry in young children. Trans Am Ophthalmol Soc. 1942;40:547-64.         

12. Irvine SR. A simple test for binocular fixation: clinical application useful in the appraisal of ocular dominance, amblyopia ex-anopsia minimal strabismus and malingering. Am J Ophthalmol. 1944;27:740-6.         

13. Bicas HEA. Medidas angulares na rotina oftalmológica: variações do efeito de prismas em função de seus posicionamentos. Rev Bras Oftalmol. 1980;39(1):5-32.         

14. Bicas HEA. Refração em dioptros planos. In: Bicas HEA, Alves AA, Uras R, editores. Refratometria ocular. Rio de Janeiro: Cultura Médica; 2005. p.41-53.         

15. Bicas HEA. Algumas considerações sobre as medidas de convergência, acomodação e relação C_A/A. Rev Latinoam Estrab. 1976;1(1):68-87.         

 

 

(1) Obviamente, o "ver" só se concretiza pelas decodificações corticais dos sinais sensorialmente iniciados pelas células fotorreceptoras da retina, isto é, percepção (visão) e cognição (relação intelectiva dos significados) são processos superiores, nunca devendo ser atribuídos ao olho. Já "olhar" significa "o olho direcionar-se a" um referencial.
(2) As frentes de onda da luz provinda de um ponto objeto do espaço objeto (externo ao olho) convergem, dentro do olho para um ponto ("imagem") que se situa efetivamente à frente da retina (no caso da miopia, divergindo a partir daí) ou, esquematicamente, atrás dela, isto é, ainda convergem ao atingir a retina (no caso da hipermetropia). De qualquer modo, tanto no caso da miopia, quanto no da hipermetropia (com a acomodação relaxada), a imagem sempre se forma na retina, embora "desfocada", por divergência dos raios luminosos (na miopia), ou por convergência incompleta deles (na hipermetropia).
(3) Cálculos foram feitos considerando a distância da fóvea ao primeiro plano principal do olho (a partir do qual a distância ao objeto é medida) como 22,4 + 0,25 = 22,65 mm. Assim, o ângulo de correção direcional (a) é calculado por a = arctan {t / (p + 22,65)}, em que t é a "translação" entre os pontos nodais e p a distância do objeto ao "olho".
(4) Sistemas ópticos mais complexos (dois ou mais dioptros) sempre se apresentam com seus elementos duplicados: dois planos focais (o objeto e o imagem), dois planos principais (o objeto e o imagem), dois pontos nodais (idem). Assim, também, uma pupila real terá sua apresentação óptica tanto no "espaço objeto" (pupila de entrada), como no "espaço imagem" (pupila de saída). De qualquer modo, para o sistema óptico do olho elas podem ser consideradas como praticamente coincidentes, falando-se, apenas, em uma "única" pupila.
(5) Pela falta de propósitos naturais para qualquer movimento ocular disjuntivo (vergência), a não ser o da convergência, a divergência absoluta é considerável como fenômeno "negativo", isto é, como resultante do relaxamento da convergência (desconvergência) na eventualidade de um desequilíbrio básico existente (exotropia, até então compensada pela convergência). Também atribuível a um relaxamento dos músculos retos mediais é a divergência fusional (reflexa) de pequena amplitude, demonstrada pela anteposição ocular de prismas de base "nasal".
(6) Os cálculos são iniciados pela conversão dos valores em dioptrias-prismáticas aos de uma unidade com que se possa trabalhar aritmeticamente - por exemplo, graus de arco; em seguida a operação é realizada; e, finalmente, os valores na unidade com que se trabalha aritmeticamente são reconvertidos aos valores em dioptrias-prismáticas. Note-se que processos de aumento (adição, multiplicação) geram valores maiores e os de redução (subtração, divisão) geram valores menores do que os simplesmente esperados se a operação aritmética direta fosse possível.
(7) Essa afirmação de impossibilidade é válida para figuras que mostrem olhos com os eixos pupilares aparentemente paralelos (pode haver desvio torcional), ou sem o referencial de fixação, ou de observação (pode haver eso ou exodesvio). Em casos de aparente esotropia, essa afirmação é também sustentável. Finalmente, a aparência de pequenos desvios divergentes, ou verticais pode ainda ser devida a distopias do eixo visual relativamente ao pupilar (ângulos kappa). Mas, obviamente, desvios divergentes e verticais de "grande" magnitude podem ser detectados por uma foto, embora não se chegue ao conhecimento de se o olho desviado seja o direito, ou o esquerdo.